
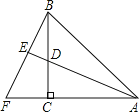
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是( )
A.4 B.3 C.2 D.1
【答案】A.
【解析】
试题分析:①∵BC=AC,∠ACB=90°,∴∠CAB=∠ABC=45°,∵AD平分∠BAC,∴∠BAE=∠EAF=22.5°,∵在Rt△ACD与Rt△BFC中,∠EAF+∠F=90°,∠FBC+∠F=90°,∴∠EAF=∠FBC,∵BC=AC,∠EAF=∠FBC,∠BCF=∠AEF,∴Rt△ADC≌Rt△BFC,∴AD=BF;
故①正确;
②∵①中Rt△ADC≌Rt△BFC,∴CF=CD,故②正确;
③∵①中Rt△ADC≌Rt△BFC,∴CF=CD,AC+CD=AC+CF=AF,∵∠CBF=∠EAF=22.5°,∴在Rt△AEF中,∠F=90°﹣∠EAF=67.5°,∵∠CAB=45°,∴∠ABF=180°﹣∠F﹣∠CAB=180°﹣67.5°﹣45°=67.5°,∴AF=AB,即AC+CD=AB,故③正确;
④由③可知,△ABF是等腰三角形,∵BE⊥AD,∴BE=![]() BF,∵在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,故BE≠CF,故④错误;
BF,∵在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,故BE≠CF,故④错误;
⑤由③可知,△ABF是等腰三角形,∵BE⊥AD,∴BF=2BE,故⑤正确.
所以①②③⑤四项正确.
故选A.


科目:初中数学 来源: 题型:
【题目】如果A和B都是5次多项式,则下面说法正确的是( )
A.A﹣B一定是多项式
B.A﹣B是次数不低于5的整式
C.A+B一定是单项式
D.A+B是次数不高于5的整式
查看答案和解析>>
科目:初中数学 来源: 题型:
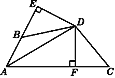
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
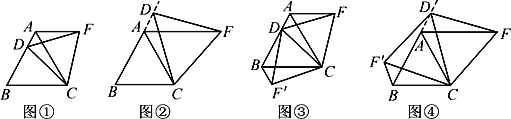
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于抛物线y=x2﹣4x+4,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.对称轴是直线线x=2
D.当x>2时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD, 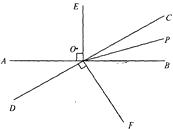
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠AOD=40°,则①∠BOC=;②OP是∠BOC的平分线,所以∠COP=度;③求∠BOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC. 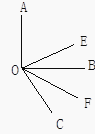
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法,保留作图痕迹):
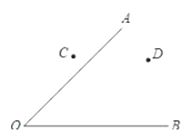
(1)尺规作图:校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P。(不写画图过程,保留作图痕迹)
用直尺和圆规在如图所示的数轴上作出表示![]() 的点.
的点.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
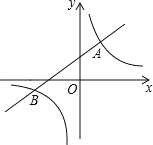
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式.
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集.
的解集.
(3)连接OA、OB,求S△ABO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com