
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC. 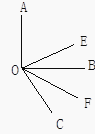
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
【答案】
(1)∵∠AOC=∠AOB+∠BOC,∴∠AOC=90°+60°=150°.∵OE平分∠AOC,∴∠EOC=150°÷2=75°.∵OF平分∠BOC,∴∠COF=60°÷2=30°.∵∠EOC=∠EOF+∠COF,∴∠EOF=75°-30°=45°.
(2)∵OE平分∠AOC,OF平分∠BOC.∴∠COE= ∠AOC,∠COF= ∠BOC∵∠AOB=∠AOC-∠BOC∴∠EOF=∠COE-∠COF= ∠AOC- ∠BOC= (∠AOC-∠BOC)= ∠AOB
(3)∵OE平分∠AOC,OF平分∠BOC,∴∠COE= ∠AOC,∠COF= ∠BOC,
∴∠EOF= ∠AOC- ∠BOC= (∠AOC-∠BOC)= ∠AOB.又∵∠AOB+∠EOF=156°,
∴∠EOF=52°.
【解析】此题难度较大,要通过角度转换.本题考查相交线所形成的角度.
【考点精析】本题主要考查了垂线的性质的相关知识点,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC引垂线,垂足分别为E、F点.
(1)当点D在BC的什么位置时,DE=DF?并证明.
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?并请给予写出(不 必证明).
(3)过C点作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是( )
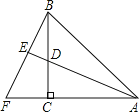
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:![]() ≈1.732)
≈1.732)
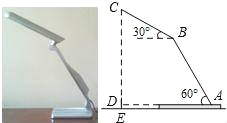
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3、﹣2、﹣1、4、5中任取两个数相加,若所得的和的最大值是a,最小值是b,则a+b的值是( )
A. ﹣2 B. ﹣3 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)与x轴一个交点在﹣1,﹣2之间,对称轴为直线x=1,图象如图,给出以下结论:①b2﹣4ac>0;②abc>0;③2a﹣b=0;④8a+c<0;⑤a+![]() b+
b+![]() c<0.其中结论正确的个数有( )
c<0.其中结论正确的个数有( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自1939年创办以来,重庆育才中学一直坚守文化底线,不断挑战自我极限,在沧桑文化中愈加根深叶茂.在今年,即将推出的本部改造计划不仅是文化审美层面的颠覆尝试,也是学校发展的巨大工程,其中三种style的民国大门各具特色,A磅礴大气,B清爽简约,C典雅古朴款,为调查民意学校让教职工进行投票呈现了四种结果,喜欢A款、喜欢B款、喜欢C款、都可以,现调查结果如下:
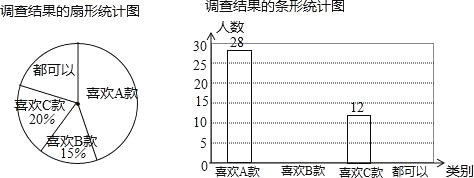
(1)如图,喜欢C款的占20%,喜欢B款的占15%,则调查总人数为,扇形统计图中认为“都可以”的所占圆心角为度;根据题中信息补全条形统计图.
(2)我们学校共有600名教职工,请根据上图估算喜欢A款的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探索
(1)填空: ![]() =______;
=______; ![]() =______;
=______; ![]() =______;
=______; ![]() ______;
______;
(2)观察第(1)题的计算结果回答: ![]() 一定等于
一定等于![]() 吗?你发现其中的规律了吗?请把你观察到的规律归纳出来 。
吗?你发现其中的规律了吗?请把你观察到的规律归纳出来 。
(3)利用你总结的规律计算: ![]() .(2<x<3)
.(2<x<3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com