练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】从﹣3、﹣2、﹣1、4、5中任取两个数相加，若所得的和的最大值是a，最小值是b，则a+b的值是（　　）

    A. ﹣2 B. ﹣3 C. 3 D. 4

    【答案】D

    【解析】

    先根据有理数的加法法则求出和的最大值和最小值，然后代入a+b计算即可.

    ∵所得的和的最大值是4+5=9，最小值是﹣3﹣2=﹣5，

    ∴a+b=9﹣5=4，

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，图②是边长为m－n的正方形．

    （1）请用图①中四个小长方形和图②中的正方形拼成一个大正方形，画出示意图(要求连接处既没有重叠，也没有空隙)；

    （2）请用两种不同的方法列代数式表示(1)中拼得的大正方形的面积；

    （3）请直接写出(m＋n)2，(m－n)2，mn这三个代数式之间的等量关系；

    （4）根据（4）中的等量关系，解决如下问题：若a＋b＝6，ab＝4，求(a－b)2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

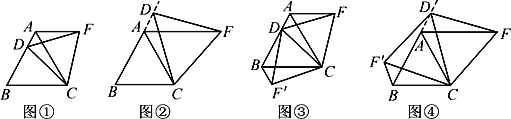
    【题目】(1)操作发现：如图①，D是等边△ABC的边BA上一动点(点D与点B不重合)，连接DC，以DC为边在BC上方作等边△DCF，连接AF，你能发现AF与BD之间的数量关系吗？并证明你发现的结论；

    (2)类比猜想：如图②，当动点D运动至等边△ABC边BA的延长线时，其他作法与(1)相同，猜想AF与BD在(1)中的结论是否仍然成立？

    (3)深入探究：Ⅰ.如图③，当动点D在等边△ABC边BA上运动时(点D与B不重合)，连接DC，以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′，连接AF，BF′，探究AF，BF′与AB有何数量关系？并证明你的探究的结论；Ⅱ.如图④，当动点D在等边△ABC的边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD，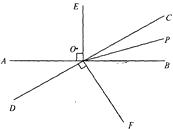
    （1）图中除直角外，还有相等的角吗？请写出两对：①；② ．
    （2）如果∠AOD＝40°，则①∠BOC＝；②OP是∠BOC的平分线，所以∠COP＝度；③求∠BOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠AOB， OE平分∠AOC， OF平分∠BOC.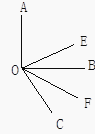
    （1）若∠AOB是直角，∠BOC＝60°，求∠EOF的度数；
    （2）猜想∠EOF与∠AOB的数量关系；
    （3）若∠AOB＋∠EOF＝156°，则∠EOF是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们学习了勾股定理后，都知道“勾三、股四、弦五”．

    观察：3、4、5；5、12、13；7、24、25；9、40、41；…，发现这些勾股数的勾都是奇数，且从3起就没有间断过．

    （1）请你根据上述的规律写出下两组勾股数：11、　　、 ； 13、　、　；

    （2）若第一个数用字母a（a为奇数，且a≥3）表示，那么后两个数用含a的代数式分别表示为　　和　　，请用所学知识说明它们是一组勾股数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】作图题（不写作法，保留作图痕迹）：

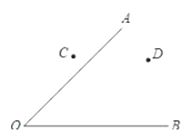
    （1）尺规作图：校园有两条路OA、OB，在交叉路口附近有两块宣传牌C、D，学校准备在这里安装一盏路灯，要求灯柱的位置P离两块宣传牌一样远，并且到两条路的距离也一样远，请你帮助画出灯柱的位置P。（不写画图过程，保留作图痕迹）

    用直尺和圆规在如图所示的数轴上作出表示的点.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y=﹣x2﹣2x+3与轴交于A、B两点，与y轴交于点C，点D为抛物线的顶点．

    （1）求直线AC的解析式，并直接写出D点的坐标．

    （2）如图1，在直线AC的上方抛物线上有一动点P，过P点作PQ垂直于x轴交AC于点Q，PM∥BD交AC于点M．

    ①求△PQM周长最大值；

    ②当△PQM周长取得最大值时，PQ与x轴交点为H，首位顺次连接P、H、O、D构成四边形，它的周长为L，若线段OH在x轴上移动，求L最小值时OH移动的距离及L的最小值．

    （3）如图2，连接BD与y轴于点F，将△BOF绕点O逆时针旋转，记旋转后的三角形为△BOF′，B′F′所在直线与直线AC、直线OC分别交于点G、K，当△CGK为直角三角形时，直接写出线段BG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】长红枣是地方特产，色泽红艳，酥脆甘甜，营养丰富，有着较高的滋补和药用价值，被誉为“天然维生素丸”．某网店以a元一包的价格购进500包长红枣，加价20%卖出400包以后，剩余每包比进价降低b元后全部卖出，则可获得利润_____元．

    查看答案和解析>>

    同步练习册答案