
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
① △ABE的面积与△BCE的面积相等;② ∠AFG=∠AGF;③ ∠FAG=2∠ACF;④ BH=CH
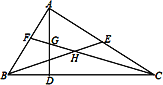
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
【答案】A
【解析】根据三角形中线的性质可得:△ABE的面积和△BCE的面积相等,故①正确,
因为∠BAC=90°,所以∠AFG+∠ACF=90°,因为AD是高,所以∠DGC+∠DCG=90°,
因为CF是角平分线,所以∠ACF=∠DCG,所以∠AFG=∠DGC,又因为∠DGC=∠AGF,所以
∠AFG=∠AGF,故②正确,
因为∠FAG+∠ABC=90°, ∠ACB+∠ABC=90°,所以∠FAG=∠ACB,又因为CF是角平分线,所以∠ACB=2∠ACF,所以∠FAG=2∠ACF,故③正确,
④假设BH=CH, ∠ACB=30°,则∠HBC=∠HCB =15°, ∠ABC=60°,
所以∠ABE=60°-15°=45°,因为∠BAC=90°,所以AB=AE,因为AE=EC,所以AB=![]() ,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
故选A.


科目:初中数学 来源: 题型:
【题目】如图,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( )
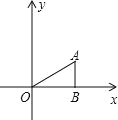
A.(﹣1,-![]() )
)
B.(﹣1,-![]() )或(﹣2,0)
)或(﹣2,0)
C.(-![]() ,﹣1)或(0,﹣2)
,﹣1)或(0,﹣2)
D.(-![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,图②是边长为m-n的正方形.
(1)请用图①中四个小长方形和图②中的正方形拼成一个大正方形,画出示意图(要求连接处既没有重叠,也没有空隙);
(2)请用两种不同的方法列代数式表示(1)中拼得的大正方形的面积;
(3)请直接写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系;
(4)根据(4)中的等量关系,解决如下问题:若a+b=6,ab=4,求(a-b)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
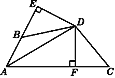
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( ). ①AB⊥AC; ②AD与AC互相垂直; ③点C到AB的垂线段是线段AB; ④点D到BC的距离是线段AD的长度; ⑤线段AB的长度是点B到AC的距离; ⑥线段AB是点B到AC的距离; ⑦AD>BD. 
A.2个
B.4个
C.7个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
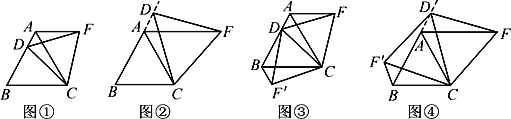
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD, 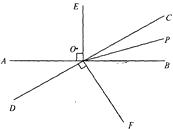
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠AOD=40°,则①∠BOC=;②OP是∠BOC的平分线,所以∠COP=度;③求∠BOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点.
(1)求直线AC的解析式,并直接写出D点的坐标.
(2)如图1,在直线AC的上方抛物线上有一动点P,过P点作PQ垂直于x轴交AC于点Q,PM∥BD交AC于点M.
①求△PQM周长最大值;
②当△PQM周长取得最大值时,PQ与x轴交点为H,首位顺次连接P、H、O、D构成四边形,它的周长为L,若线段OH在x轴上移动,求L最小值时OH移动的距离及L的最小值.
(3)如图2,连接BD与y轴于点F,将△BOF绕点O逆时针旋转,记旋转后的三角形为△BOF′,B′F′所在直线与直线AC、直线OC分别交于点G、K,当△CGK为直角三角形时,直接写出线段BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com