
【题目】已知在△ABC中,AB=AC在射线AC上取一点D,以D为顶点、DB为一条边作∠BDF=∠A,点E在AC的延长线上,∠ECF=∠ACB
(1)如图(1),当点D在边AC上时,求证:①∠FDC=∠ABD②DB=DF
(2)如图(2),当点D在AC的延长线上时,请判断DB与DF是否相等,并说明理由

【答案】(1)①证明见解析;②证明见解析;(2)相等,理由见解析.
【解析】
(1)①利用外角定理及角的和差关系即可证明;
②过点D分别作DM垂直BC于M ,DN垂直CF交FC的延长线于N,先证明△DMC≌△DNC,再证明△DBM≌△DFN,最后利用全等的性质即可得到结果;
(2)过点D分别作DP垂直CF于P ,DQ垂直BC交BC的延长线于Q,先证明△DPC≌△DQC,再证明△DPF≌△DQB,最后利用全等的性质即可得到结果.
(1)证明:①∵∠BDC=∠A+∠ABD,∠BDC=∠BDF+∠FDC,且∠A=∠BDF,
∴∠FDC=∠ABD;
②过点D分别作DM垂直BC于M ,DN垂直CF交FC的延长线于N,

∴∠DMB=∠DMC=90°,∠DNC=∠DNF=90°,
∴∠DMC=∠DNC=90°,
∵∠ECF=∠ACB,∠ECF=∠ACN (对顶角相等),
∴∠ACB=∠ACN,
又∵CD=CD,
∴△DMC≌△DNC (AAS),
∴DM=DN,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=∠ECF,
∵∠ECF=∠FDC+∠DFN,∠ABC=∠ABD+∠DBM,
且由①知,∠FDC=∠ABD,
∴∠DBM=∠DFN,
又∵∠DMB=∠DNF=90°,
∴△DBM≌△DFN (AAS),
∴DB=DF;
(2)解:DB=DF,理由如下:
过点D分别作DP垂直CF于P ,DQ垂直BC交BC的延长线于Q,

∴∠DPC=∠DPF=90°,∠DQC=∠DQB=90°,
∴∠DPC=∠DQC=90°,∠DPF=∠DQB=90°,
∵∠ACB=∠DCQ (对顶角相等),∠ACB=∠ECF,
∴∠ECF=∠DCQ,
∵CD=CD,
∴△DPC≌△DQC (AAS),
∴DP=DQ,
∵∠BDE=∠ABD+∠A,∠BDE=∠BDF+∠EDF,且∠BDF=∠A,
∴∠ABD=∠EDF,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=∠ECF,
∵∠ABD=∠ABC+∠DBQ,∠EDF=∠ECF+∠DFP,
∴∠DBQ=∠DFP,
∴△DPF≌△DQB (AAS),
∴DB=DF.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,AB=10,AC=6,求△ADE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() ,点
,点![]() 为射线
为射线![]() 上一点,延长
上一点,延长![]() 至点
至点![]() ,使得
,使得![]() ,联结
,联结![]() 并延长交射线
并延长交射线![]() 于点
于点![]() 。
。
(1)当点![]() 在边
在边![]() 上时,如图1,若
上时,如图1,若![]() ,则
,则![]()
(2)当点![]() 在边
在边![]() 上时,如图2,若
上时,如图2,若![]() ,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。
(3)当点![]() 在边
在边![]() 的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象过点A(4,1)与正比例函数
的图象过点A(4,1)与正比例函数![]() (
(![]() )的图象相交于点B(
)的图象相交于点B(![]() ,3),与
,3),与![]() 轴相交于点C.
轴相交于点C.
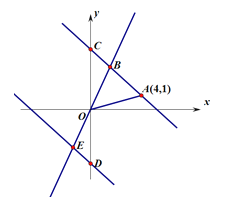
(1)求一次函数和正比例函数的表达式;
(2)若点D是点C关于![]() 轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
(3)在坐标轴上是否存在一点![]() ,使
,使![]() .若存在请求出点
.若存在请求出点![]() 的坐标,若不存在请说明理由.
的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形的中心在原点![]() ,且正方形的一组对边与
,且正方形的一组对边与![]() 轴平行.点
轴平行.点![]() 是反比例幽数
是反比例幽数![]() 的图象上与正方形的一个交点,若图中阴影部分的面积等于
的图象上与正方形的一个交点,若图中阴影部分的面积等于![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)是燃烧时间x(h) 的一次函数.某蜡烛的高度为30cm,燃烧3h后,蜡烛剩余部分的高度为12cm.
(1)求蜡烛燃烧时y(cm)与x(h)之间的函数表达式;
(2)求出蜡烛从点燃到燃尽所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ﹙
﹙![]() ,
,![]() ﹚,
﹚,![]() ﹙
﹙![]() ,
,![]() ﹚,交
﹚,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.

![]() 求反比例函数
求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
![]() 连接
连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
![]() 根据图象写出使一次函数的值小于反比例函数的值的
根据图象写出使一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义感知:我们把顶点关于![]() 轴对称,且交于
轴对称,且交于![]() 轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线
轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线![]() 与
与![]() 是一对“孪生抛物线”,其“共点”为点
是一对“孪生抛物线”,其“共点”为点![]() .
.
初步运用:
![]() 判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“
判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“![]() ”:
”:
①“孪生抛物线”的“共点”不能分布在![]() 轴上.________
轴上.________
②“孪生抛物线”![]() 与
与![]() 的“共点”坐标为
的“共点”坐标为![]() .________
.________
![]() 填空:抛物线
填空:抛物线![]() 的“孪生抛物线”的解析式为________.
的“孪生抛物线”的解析式为________.
延伸拓展:在平面直角坐标系中,记“孪生抛物线”的两顶点分别为![]() ,
,![]() ,且
,且![]() ,其“共点”
,其“共点”![]() 与
与![]() ,
,![]() ,
,![]() 三点恰好构成一个面积为
三点恰好构成一个面积为![]() 的菱形,试求该“孪生抛物线”的解析式.
的菱形,试求该“孪生抛物线”的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过点
的图象过点![]() 和点
和点![]() ,对称轴为直线
,对称轴为直线![]() .
.

![]() 求该二次函数的关系式和顶点坐标;
求该二次函数的关系式和顶点坐标;
![]() 结合图象,解答下列问题:
结合图象,解答下列问题:
①当![]() 时,求函数
时,求函数![]() 的取值范围.
的取值范围.
②当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com