
【题目】如图,等边![]() ,点
,点![]() 为射线
为射线![]() 上一点,延长
上一点,延长![]() 至点
至点![]() ,使得
,使得![]() ,联结
,联结![]() 并延长交射线
并延长交射线![]() 于点
于点![]() 。
。
(1)当点![]() 在边
在边![]() 上时,如图1,若
上时,如图1,若![]() ,则
,则![]()
(2)当点![]() 在边
在边![]() 上时,如图2,若
上时,如图2,若![]() ,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。
(3)当点![]() 在边
在边![]() 的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。

【答案】(1)60°;(2)见解析;(3)∠CFA+∠DBC=60°,理由见解析.
【解析】
(1)由等边三角形的性质可得BD⊥AE,∠DBE=∠DBA=30°,AB=AE,可求∠CFA=∠ABC+∠ECD=90°,即可求解;
(2)如图2,过点C作CH∥AB交AE的延长线于H,可证△CHE是等边三角形,可得CH=CE=HE=AD,通过证明△BAD≌△DHC,可得∠DBF=∠HDC,由外角性质可求解;
(3)如图3,过点C作CH∥AB交AE的延长线于H,可证△CHE是等边三角形,可得CH=CE=HE=AD,通过证明△BAD≌△DHC,可得∠DBF=∠HDC,由外角性质可求解;
(1)∵△ABE是等边三角形,ED=AD,
∴BD⊥AE,∠DBE=∠DBA=30°,AB=AE,
∵EC=AD,∠BEA=60°,
∴∠ECF=30°,
∴∠CFA=∠ABC+∠ECD=90°,
∴∠CFA-∠DBC=90°-30°=60°,
故答案为:60°;
(2)如图2,过点C作CH∥AB交AE的延长线于H,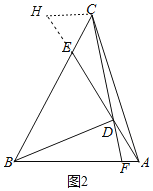
∵CH∥AB,
∴∠H=∠EAB=60°,∠HCE=∠EBA=60°,
∴△CHE是等边三角形,
∴CH=CE=HE,
∵EC=AD,
∴HE=CH=AD,
∴HE+DE=AD+DE,
∴HD=AE=AB,
∵HD=AB,AD=CH,∠H=∠BAD=60°,
∴△BAD≌△DHC(SAS)
∴∠DBF=∠HDC,
∵∠CFA=∠CBF+∠BCF=∠CBD+∠DBF+∠BCF,
∴∠CFA-∠DBC=∠DBF+∠BCF=∠HDC+∠BCF=∠BEA=60°;
(3)如图3,过点C作CH∥AB交AE的延长线于H,
∵CH∥AB,
∴∠HCD=∠CFA,∠H=∠EAB=60°,∠HCE=∠EBA=60°,
∴△CHE是等边三角形,
∴CH=CE=HE,
∵EC=AD,
∴HE=CH=AD,
∴HE-DE=AD-DE,
∴HD=AE=AB,
∵HD=AB,AD=CH,∠H=∠BAD=60°,
∴△BAD≌△DHC,(SAS)
∴∠DBA=∠HDC,∠HCD=∠BDA,
∴∠BDA=∠CFA,
∵∠AEB=∠ADB+∠DBC=60°,
∴∠CFA+∠DBC=60°.


科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,中超十一轮,重庆力帆将主场迎战河北华夏幸福,重庆“铁血巴渝”球迷协会将继续组织铁杆球迷到现场为重庆力帆加油助威.“铁血巴渝”球迷协会计划购买甲、乙两种球票共
日,中超十一轮,重庆力帆将主场迎战河北华夏幸福,重庆“铁血巴渝”球迷协会将继续组织铁杆球迷到现场为重庆力帆加油助威.“铁血巴渝”球迷协会计划购买甲、乙两种球票共![]() 张,并且甲票的数量不少于乙票的
张,并且甲票的数量不少于乙票的![]() 倍.
倍.
![]() 求“铁血巴渝”球迷协会至少购买多少张甲票;
求“铁血巴渝”球迷协会至少购买多少张甲票;
![]() “铁血巴渝”球迷协会从售票处得知,售票处将给予球迷协会一定的优惠,本场比赛球票以统一价格
“铁血巴渝”球迷协会从售票处得知,售票处将给予球迷协会一定的优惠,本场比赛球票以统一价格![]() 元出售给该协会,因此协会决定购买的票数将在原计划的基础上增加
元出售给该协会,因此协会决定购买的票数将在原计划的基础上增加![]() ,购票后总共用去
,购票后总共用去![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状和大小完全相同的正方形网格纸,正方形网格中每个小正方形的边长为1,线段AC的两个端点均在小正方形的顶点上.

(1)在图1中画出△ABC,使△ABC是以AC为腰的等腰直角三角形,点B在小正方形的顶点上;
(2)在图2中画出△ADC,使△ADC是以AD为腰的等腰三角形,点D在小正方形的顶点上,且△ADC的面积为10.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中

(1)写出△ABC的顶点坐标,并求出△ABC的面积;
(2)画出△ABC关于y轴对称的图形△A1B1C1并写出各顶点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义![]() 为函数
为函数![]() 的特征数,下面给出特征数为
的特征数,下面给出特征数为![]() 的函数的一些结论:
的函数的一些结论:
①当![]() 时,函数图象的顶点坐标是
时,函数图象的顶点坐标是![]() ;
;
②当![]() 时,函数图象截
时,函数图象截![]() 轴所得的线段长度大于
轴所得的线段长度大于![]() ;
;
③当![]() 时,函数在
时,函数在![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
④当![]() 时,函数图象经过同一个点.
时,函数图象经过同一个点.
其中正确的结论有( )
A. ①②③④ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC在射线AC上取一点D,以D为顶点、DB为一条边作∠BDF=∠A,点E在AC的延长线上,∠ECF=∠ACB
(1)如图(1),当点D在边AC上时,求证:①∠FDC=∠ABD②DB=DF
(2)如图(2),当点D在AC的延长线上时,请判断DB与DF是否相等,并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计建造一条道路,路基的横断面为梯形ABCD,如图(单位:米).设路基高为h,两侧的坡角分别为![]() 和
和![]() ,已知h=2,
,已知h=2,![]() ,
,![]() ,
,![]() .
.
(1)求路基底部AB的宽;
(2)修筑这样的路基1000米,需要多少土石方?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com