
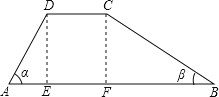
【题目】设计建造一条道路,路基的横断面为梯形ABCD,如图(单位:米).设路基高为h,两侧的坡角分别为![]() 和
和![]() ,已知h=2,
,已知h=2,![]() ,
,![]() ,
,![]() .
.
(1)求路基底部AB的宽;
(2)修筑这样的路基1000米,需要多少土石方?

【答案】(1)16米;(2)26000立方米.
【解析】
(1)分别过D、C作下底AB的垂线,设垂足为E、F.在Rt△ADE和Rt△BCF中,可根据h的长以及坡角的度数或坡比的值,求出AE、BF的长,进而可求得AB的值.
(2)根据(1)得出的梯形下底宽,可求出梯形的面积,进而可求出需要多少土石方.
(1)过D作DE⊥AB于E,过C作CF⊥AB于F.
Rt△ADE中,∠α=45°,DE=h=2,
∴AE=DE=h=2.
Rt△BCF中,tanβ=![]() ,CF=h=2,
,CF=h=2,
∴BF=2CF=4.
故AB=AE+EF+BF=AE+CD+BF=2+10+4=16.
(2)S梯形ABCD=![]() (AB+CD)h=
(AB+CD)h=![]() ×(10+16)×2=26.
×(10+16)×2=26.
因此所需的土石方数是:26×1000=26000(立方米).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,等边![]() ,点
,点![]() 为射线
为射线![]() 上一点,延长
上一点,延长![]() 至点
至点![]() ,使得
,使得![]() ,联结
,联结![]() 并延长交射线
并延长交射线![]() 于点
于点![]() 。
。
(1)当点![]() 在边
在边![]() 上时,如图1,若
上时,如图1,若![]() ,则
,则![]()
(2)当点![]() 在边
在边![]() 上时,如图2,若
上时,如图2,若![]() ,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。
(3)当点![]() 在边
在边![]() 的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ﹙
﹙![]() ,
,![]() ﹚,
﹚,![]() ﹙
﹙![]() ,
,![]() ﹚,交
﹚,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.

![]() 求反比例函数
求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
![]() 连接
连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
![]() 根据图象写出使一次函数的值小于反比例函数的值的
根据图象写出使一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义感知:我们把顶点关于![]() 轴对称,且交于
轴对称,且交于![]() 轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线
轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线![]() 与
与![]() 是一对“孪生抛物线”,其“共点”为点
是一对“孪生抛物线”,其“共点”为点![]() .
.
初步运用:
![]() 判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“
判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“![]() ”:
”:
①“孪生抛物线”的“共点”不能分布在![]() 轴上.________
轴上.________
②“孪生抛物线”![]() 与
与![]() 的“共点”坐标为
的“共点”坐标为![]() .________
.________
![]() 填空:抛物线
填空:抛物线![]() 的“孪生抛物线”的解析式为________.
的“孪生抛物线”的解析式为________.
延伸拓展:在平面直角坐标系中,记“孪生抛物线”的两顶点分别为![]() ,
,![]() ,且
,且![]() ,其“共点”
,其“共点”![]() 与
与![]() ,
,![]() ,
,![]() 三点恰好构成一个面积为
三点恰好构成一个面积为![]() 的菱形,试求该“孪生抛物线”的解析式.
的菱形,试求该“孪生抛物线”的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在一次高尔夫球争霸赛中从山坡上的点![]() 打出一球向球洞
打出一球向球洞![]() 飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度
飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度![]() 时,球移动的水平距离为
时,球移动的水平距离为![]() .已知山坡
.已知山坡![]() 与水平方向
与水平方向![]() 的夹角为
的夹角为![]() ,
,![]() ,
,![]() 两点相距
两点相距![]()
![]() .
.
![]() 求出点
求出点![]() 的坐标;
的坐标;
![]() 求抛物线解析式.并判断小明这一杆能否把高尔夫球从点
求抛物线解析式.并判断小明这一杆能否把高尔夫球从点![]() 直接打入球洞
直接打入球洞![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 和
和![]() ,下列关于此二次函数的叙述,正确的是( )
,下列关于此二次函数的叙述,正确的是( )

A. 当![]() 时,
时,![]() 的值小于
的值小于![]()
B. 当![]() 时,
时,![]() 的值大于
的值大于![]()
C. 当![]() 时,
时,![]() 的值等于
的值等于![]()
D. 当![]() 时,
时,![]() 的值大于
的值大于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )
,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )

A. ①②③④ B. ②③④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过点
的图象过点![]() 和点
和点![]() ,对称轴为直线
,对称轴为直线![]() .
.

![]() 求该二次函数的关系式和顶点坐标;
求该二次函数的关系式和顶点坐标;
![]() 结合图象,解答下列问题:
结合图象,解答下列问题:
①当![]() 时,求函数
时,求函数![]() 的取值范围.
的取值范围.
②当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬天,小芳给自己家刚刚装满水且显示温度为![]() 的太阳能热水器里的水加热.她每过一段时间去观察一下显示温度,并记录如下:
的太阳能热水器里的水加热.她每过一段时间去观察一下显示温度,并记录如下:
时间(分钟) | 0 | 5 | 10 | 15 | 20 | …… |
显示温度( | 16 | 17 | 18 | 19 | 20 | …… |
(1)请直接写出显示温度(![]() )与加热时间(
)与加热时间(![]() )之间的函数关系式;
)之间的函数关系式;
(2)如果她给热水器设定的最高温度为![]() ,问:要加热多长时间才能达到设定的最高温度?
,问:要加热多长时间才能达到设定的最高温度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com