【题目】如图，在△ABC中，∠ABC与∠ACB的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E，AB＝10，AC＝6，求△ADE的周长．
【答案】16
【解析】
根据角平分线的定义可得：∠DBO=∠CBO，∠ECO=∠BCO，再根据平行的性质可得∠DOB=∠CBO，∠EOC=∠BCO，从而证出∠DBO=∠DOB，∠ECO=∠EOC，根据等角对等边即可得：DB=DO，EC =EO，计算△ADE的周长即可.
解：∵∠ABC与∠ACB的平分线交于点O
∴∠DBO=∠CBO，∠ECO=∠BCO
∵DE∥BC
∴∠DOB=∠CBO，∠EOC=∠BCO
∴∠DBO=∠DOB，∠ECO=∠EOC
∴DB=DO，EC =EO
∴△ADE的周长= AD+DE＋AE = AD+DO＋EO＋AE= AD+ DB＋EC＋AE=AB＋AC=10＋6=16
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A（0，b）、点B（a，0）、点D（d，0）且a、b、c满足
．DE⊥x轴且∠BED=∠ABD，BE交y轴于点C，AE交x轴于点F．
（1）求点A、B、D的坐标；
（2）求点C、E、F的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
年
月
日，中超十一轮，重庆力帆将主场迎战河北华夏幸福，重庆“铁血巴渝”球迷协会将继续组织铁杆球迷到现场为重庆力帆加油助威．“铁血巴渝”球迷协会计划购买甲、乙两种球票共
张，并且甲票的数量不少于乙票的
倍．
求“铁血巴渝”球迷协会至少购买多少张甲票；
“铁血巴渝”球迷协会从售票处得知，售票处将给予球迷协会一定的优惠，本场比赛球票以统一价格
元出售给该协会，因此协会决定购买的票数将在原计划的基础上增加
，购票后总共用去
元，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果三角形有一边上的中线长恰好等于这边的长，那么这个三角形叫“恰等三角形”，这条中线叫“恰等中线”．
（直角三角形中的“恰等中线”）
（1）如图1，在△ABC中，∠C＝90°，AC＝
，BC＝2，AM为△ABC的中线．求证：AM是“恰等中线”．
（等腰三角形中的“恰等中线”）
（2）已知，等腰△ABC是“恰等三角形”，AB＝AC＝20，求底边BC的平方．
（一般三角形中的“恰等中线”）
（3）如图2，若AM是△ABC的“恰等中线”，则BC2，AB2，AC2之间的数量关系为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正八边形ABCDEFGH的边长为a，I、J、K、L分别是各自所在边的中点，且四边形IJKL是正方形，则正方形IJKL的边长为________（用含a的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
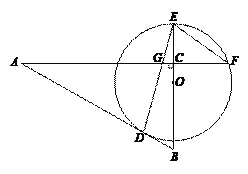
【题目】Rt△ABC中，∠ACB＝90°，AC:BC＝4:3，O是BC上一点，⊙O交AB于点D，交BC延长线于点E．连接ED，交AC于点G，且AG＝AD．
（1）求证：AB与⊙O相切；
（2）设⊙O与AC的延长线交于点F，连接EF，若EF∥AB，且EF＝5，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1，图2是两张形状和大小完全相同的正方形网格纸，正方形网格中每个小正方形的边长为1，线段AC的两个端点均在小正方形的顶点上．
（1）在图1中画出△ABC，使△ABC是以AC为腰的等腰直角三角形，点B在小正方形的顶点上；
（2）在图2中画出△ADC，使△ADC是以AD为腰的等腰三角形，点D在小正方形的顶点上，且△ADC的面积为10．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在△ABC中，AB＝AC在射线AC上取一点D，以D为顶点、DB为一条边作∠BDF＝∠A，点E在AC的延长线上，∠ECF＝∠ACB
(1)如图(1)，当点D在边AC上时，求证:①∠FDC＝∠ABD②DB＝DF
(2)如图(2)，当点D在AC的延长线上时，请判断DB与DF是否相等，并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
