
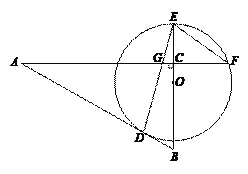
【题目】Rt△ABC中,∠ACB=90°,AC:BC=4:3,O是BC上一点,⊙O交AB于点D,交BC延长线于点E.连接ED,交AC于点G,且AG=AD.
(1)求证:AB与⊙O相切;
(2)设⊙O与AC的延长线交于点F,连接EF,若EF∥AB,且EF=5,求BD的长.
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)连结OD,由∠ACB=90°,可得∠OED+∠EGC=90°,再由OD=OE,根据等腰三角形的性质可得∠ODE=∠OED,再因AG=AD,根据等腰三角形的性质可得∠ADG=∠AGD ,由∠OED+∠EGC=∠ADG+∠ODE=∠ADO=90°,可得OD⊥AB ,所以AB是⊙O的切线;(2)连接OF,由EF∥AB,AC:BC=4:3,可得CF:CE=4:3.在Rt△ECF中,EF=5,求得CF=4,CE=3.设半径=r,则OF=r,CF=4,CO=r-3.
在Rt△OCF中,由勾股定理求得r=![]() , 再证得△CEF∽△DBO,根据相似三角形的性质可得
, 再证得△CEF∽△DBO,根据相似三角形的性质可得![]() ,由此求得BD=
,由此求得BD=![]() .
.
详解:
(1)证明:连结OD
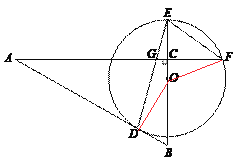
∵∠ACB=90°,
∴∠OED+∠EGC=90°,
∴OD=OE,
∴∠ODE=∠OED,
∵AG=AD,
∴∠ADG=∠AGD ,
∵∠AGD=∠EGC,
∴∠OED+∠EGC=∠ADG+∠ODE=∠ADO=90°,
∴OD⊥AB ,
∵OD为半径,
∴AB是⊙O的切线;
(2)连接OF.
∵EF∥AB,AC:BC=4:3,
∴CF:CE=4:3.
又∵EF=5,
∴CF=4,CE=3.
设半径=r,则OF=r,CF=4,CO=r-3.
在Rt△OCF中,由勾股定理,可得r=![]() .
.
∵EF∥AB,
∴∠CEF=∠B,
∴△CEF∽△DBO,
∴![]() =
=![]() ,
,
∴BD=![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形中,顶角等于![]() 的等腰三角形称为黄金三角形,如图
的等腰三角形称为黄金三角形,如图![]() ,在
,在![]() 中,已知:
中,已知:![]() ,且
,且![]() .
.
![]() 在图
在图![]() 中,用尺规作
中,用尺规作![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,并连接
,并连接![]() (保留作图痕迹,不写作法);
(保留作图痕迹,不写作法);
![]() 是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;
是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;
![]() 设
设![]() ,试求
,试求![]() 的值;
的值;
![]() 如图
如图![]() ,在
,在![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )

A.(0,﹣4)B.(﹣2,0)C.(2,4)D.(﹣2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,AB=10,AC=6,求△ADE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A![]() 、B
、B![]() 、C
、C![]() ;左视图分别是A
;左视图分别是A![]() 、B
、B![]() 、C
、C![]() ;俯视图分别是A3、B3、C3.
;俯视图分别是A3、B3、C3.
(1)请你分别写出A![]() 、A
、A![]() 、A
、A![]() 、B
、B![]() 、B
、B![]() 、B
、B![]() 、C
、C![]() 、C
、C![]() 、C
、C![]() 图形的名称;
图形的名称;
(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A![]() 、A
、A![]() 、A
、A![]() 的三张卡片放在甲口袋中,画有B
的三张卡片放在甲口袋中,画有B![]() 、B
、B![]() 、B
、B![]() 的三张卡片放在乙口袋中,画有C
的三张卡片放在乙口袋中,画有C![]() 、C
、C![]() 、C
、C![]() 的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.
的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.
①画出树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率;
②小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜.这个游戏对双方公平吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
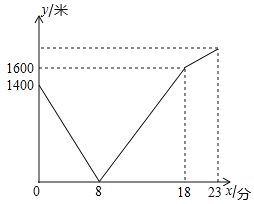
【题目】小婷家与学校之间是一条笔直的公路,小婷从家步行前往学校的途中发现忘记带昨天的回家作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小婷沿原路返回![]() 两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
![]() 妈妈从家出发______分钟后与小婷相遇;
妈妈从家出发______分钟后与小婷相遇;
![]() 相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米
相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)是燃烧时间x(h) 的一次函数.某蜡烛的高度为30cm,燃烧3h后,蜡烛剩余部分的高度为12cm.
(1)求蜡烛燃烧时y(cm)与x(h)之间的函数表达式;
(2)求出蜡烛从点燃到燃尽所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com