
����Ŀ����ͼ1��ʾ����һ��������ֽƬABC����֪��ACB=90��,AC=24,BC=10,AB=26,��DΪAB����һ�㣬����CD��AD=CD=DB����CD������ֽƬ������![]() ����
����![]() ������������ͼ2��ʾ����ֽƬ��
������������ͼ2��ʾ����ֽƬ��![]() ��ֱ��
��ֱ��![]() ����ƽ�ƣ���A��
����ƽ�ƣ���A��![]() ʼ�ն���ͬһֱ���ϣ���
ʼ�ն���ͬһֱ���ϣ���![]() ��
��![]() ���ڵ�E��
���ڵ�E��![]() ��
��![]() ��
��![]() �ֱ��ڵ�E��F��
�ֱ��ڵ�E��F��
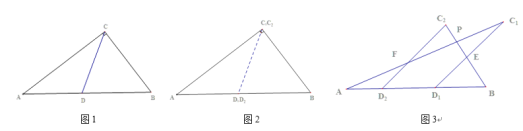
��1������A![]() ƽ�ƹ����У���֤��
ƽ�ƹ����У���֤��![]()
��2������A![]() ƽ�Ƶ���ͼ3��ʾ��λ��ʱ������ͼ�е�
ƽ�Ƶ���ͼ3��ʾ��λ��ʱ������ͼ�е�![]() ������ϵ��������֤����
������ϵ��������֤����
��3����ƽ�ƾ���![]() Ϊx����ƽ�ƹ����У�AP=
Ϊx����ƽ�ƹ����У�AP=![]() AB��PB=
AB��PB=![]() AB���������APB���������ԭ��ABC���һ��ʱ��xֵ��
AB���������APB���������ԭ��ABC���һ��ʱ��xֵ��
���𰸡���1������������2��D1E��D2F��֤������������3��![]() .
.
��������
��1������ƽ�Ƶ����ʿɵ�AC��AC1��Ȼ���ϡ�ACB=90����֤�ý��ۣ�
��2������ƽ���ߵ����ʺ͵ȱ߶ԵȽǿɵá�AFD2����A��Ȼ��ɵ�AD2��D2F��ͬ�����BD1��D1E��Ȼ�������߶κͲ�֤��AD2��BD1���ɵõ�D1E��D2F��
��3������ƽ�ƾ���Ϊx�ɵ�AB��26-x��Ȼ���ʾ��AP��PB��������APB���������ԭ��ABC���һ���г����̲���⣬��ȥ���������ֵ���ɵó����.
�⣺��1������ƽ�Ƶ����ʿɵ�AC��AC1��
�ߡ�ACB=90������AC��BC��
��AC1��BC����![]() ��
��
��2��D1E��D2F��
֤������C1D1��C2D2��
���C1����AFD2��
�֡�AD=CD=DB����C1D1��C2D2��BD2��AD1��
���C1����A��
���AFD2����A��
��AD2��D2F��
ͬ����BD1��D1E��
�֡�AD1��BD2��
��AD2��BD1��
��D1E��D2F��
��3����ƽ�ƾ���![]() Ϊx��
Ϊx��
��AB��26-x��
��AP=![]() AB=
AB=![]() ��PB=
��PB=![]() AB=
AB=![]() ��
��
������ã�![]() ��
��
�����ã�![]() ��
��
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
����APB���������ԭ��ABC���һ��ʱ��xֵΪ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������֪�����ǰѶ������![]() ��Գƣ��ҽ���
��Գƣ��ҽ���![]() ����ͬһ������������߽��������������������õ������������������������������ͼ��ʾ��������
����ͬһ������������߽��������������������õ������������������������������ͼ��ʾ��������![]() ��
��![]() ��һ����������������������������Ϊ��
��һ����������������������������Ϊ��![]() ��
��
�������ã�
![]() �ж������۶��Ƿ���ȷ����ȷ�����������ϴ����̡�������������
�ж������۶��Ƿ���ȷ����ȷ�����������ϴ����̡�������������![]() ����
����
�١��������������������������ֲܷ���![]() ���ϣ�________
���ϣ�________
�ڡ�������������![]() ��
��![]() ��������������Ϊ
��������������Ϊ![]() ��________
��________
![]() ��գ�������
��գ�������![]() �����������������Ľ���ʽΪ________��
�����������������Ľ���ʽΪ________��
������չ����ƽ��ֱ������ϵ�У�������������������������ֱ�Ϊ![]() ��
��![]() ����
����![]() ������������
������������![]() ��
��![]() ��
��![]() ��
��![]() ����ǡ�ù���һ�����Ϊ
����ǡ�ù���һ�����Ϊ![]() �����Σ���������������������Ľ���ʽ��
�����Σ���������������������Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���![]() ��ͼ�����
��ͼ�����![]() �͵�
�͵�![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ��
��

![]() ��ö��κ����Ĺ�ϵʽ�Ͷ������ꣻ
��ö��κ����Ĺ�ϵʽ�Ͷ������ꣻ
![]() ���ͼ����������⣺
���ͼ����������⣺
�ٵ�![]() ʱ������
ʱ������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڵ�![]() ʱ����
ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ת�̱����ֳ�������ͬ��С�����Σ����ֱ����1��2��3��4��5��6���������֣�ָ��ͣ��ÿ�����εĿ�������ȡ���λͬѧ���Է������������⣺
�ף����ָ��ǰ���ζ�ͣ����3�����Σ��´ξ�һ������ͣ��3�����Σ�
�ң�ֻҪָ������ת���Σ�һ������һ��ͣ��6�����Σ�
����ָ��ͣ�����������εĸ�����ͣ��ż�������εĸ�����ȣ�
���������õ�ʱ��ֻҪ��ת��ǰĬĬ�����ָ��ͣ��6�����Σ�ָ��ͣ��6�����εĿ����Ծͻ�Ӵ�
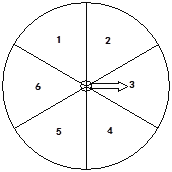
���У�����Ϊ��ȷ�ļ����У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬AC��BC������C�ڡ�ABC����ֱ��MN��AM��NN�ڵ�M��BN��MN��N��
��1����֤����AMC�ա�CNB��
��2����֤��MN��AM+BN��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֽ���ʽ��
��1��3x2��6xy+3y2
��2����3x3y2+6x2y3��3xy4
��3��4a2��25b2
��4����2x+3y����2x��y����y��2x��y��
��5��x3��4x
��6����m+1����m��9��+8m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����죬С�����Լ��Ҹո�װ��ˮ����ʾ�¶�Ϊ![]() ��̫������ˮ�����ˮ����.��ÿ��һ��ʱ��ȥ�۲�һ����ʾ�¶ȣ�����¼���£�
��̫������ˮ�����ˮ����.��ÿ��һ��ʱ��ȥ�۲�һ����ʾ�¶ȣ�����¼���£�
ʱ�䣨���ӣ� | 0 | 5 | 10 | 15 | 20 | ���� |
��ʾ�¶ȣ� | 16 | 17 | 18 | 19 | 20 | ���� |
��1����ֱ��д����ʾ�¶ȣ�![]() �������ʱ�䣨
�������ʱ�䣨![]() ��֮��ĺ�����ϵʽ��
��֮��ĺ�����ϵʽ��
��2�����������ˮ���趨������¶�Ϊ![]() ���ʣ�Ҫ���ȶʱ����ܴﵽ�趨������¶ȣ�
���ʣ�Ҫ���ȶʱ����ܴﵽ�趨������¶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������Ϸ�����ɼ�дһ�����������Ҳ¼�д������Ҫ������д�Ͳµ�����ֻ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����������
�����������
![]() �����б�������״ͼ��ʾ������д�Ͳµ����������
�����б�������״ͼ��ʾ������д�Ͳµ����������
![]() �������д�Ͳµ�������ͬ�����������������ͨ������������������ͨ���ĸ��ʣ�
�������д�Ͳµ�������ͬ�����������������ͨ������������������ͨ���ĸ��ʣ�
![]() �����д�����ּ�Ϊ
�����д�����ּ�Ϊ![]() �����Ҳµ����ּ�Ϊ
�����Ҳµ����ּ�Ϊ![]() ��������д�Ͳµ���������
��������д�Ͳµ���������![]() �����������������Ϭ������������������Ϭ���ĸ��ʣ�
�����������������Ϭ������������������Ϭ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ�ǡ�ABC�У���C=90������O��AB���е㣬��AB=![]() ����һ��ֱ�����ǰ��ֱ�Ƕ�����ڵ�O����ʼ�ձ��ָ����ǰ����ֱ�DZ߷ֱ���AB��BC�ཻ������ֱ�ΪD��E����CD+CE=�� ��
����һ��ֱ�����ǰ��ֱ�Ƕ�����ڵ�O����ʼ�ձ��ָ����ǰ����ֱ�DZ߷ֱ���AB��BC�ཻ������ֱ�ΪD��E����CD+CE=�� ��

A.![]() B.
B.![]() C.2D.
C.2D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com