
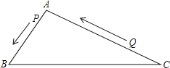
【题目】如图,![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 厘米的速度向
厘米的速度向![]() 运动,点
运动,点![]() 从
从![]() 同时出发,以每秒
同时出发,以每秒![]() 厘米的速度向
厘米的速度向![]() 运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以
运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,运动时间为________.
相似时,运动时间为________.
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-![]() x+8的图像与x轴、y轴分别交于A、B两点.P是x轴上一个动点,若沿BP将△OBP翻折,点O恰好落在直线AB上的点C处,则点P的坐标是______.
x+8的图像与x轴、y轴分别交于A、B两点.P是x轴上一个动点,若沿BP将△OBP翻折,点O恰好落在直线AB上的点C处,则点P的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 过
过![]() 轴上的点
轴上的点![]() ,且与抛物线
,且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 点坐标为
点坐标为![]() .
.
![]() 求直线和抛物线所表示的函数表达式;
求直线和抛物线所表示的函数表达式;
![]() 在抛物线上是否存在一点
在抛物线上是否存在一点![]() ,使得
,使得![]() ?若不存在,说明理由;若存在,请求出点
?若不存在,说明理由;若存在,请求出点![]() 的坐标,与同伴交流.
的坐标,与同伴交流.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在学习了《勾股定理》和《实数》后,某班同学以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动.
操作发现
“毕达哥拉斯”小组的同学想到借助正方形网格解决问题.如图1是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C、A,他们借助此图求出了△ABC的面积.

(1)在图1中,所画的△ABC的三边长分别是AB= ,BC= ,AC= ; △ABC的面积为 .
实践探究
(2)在图2所示的正方形网格中画出△DEF(顶点都在格点上),使DE=![]() ,DF=
,DF=![]() , EF=
, EF=![]() ,并写出△DEF的面积.
,并写出△DEF的面积.
继续探究
“秦九韶”小组的同学想到借助曾经阅读的数学资料: 已知三角形的三边长分别为a、b、c,求其面积,对此问题中外数学家曾经进行过深入研究.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式:
![]()
我国南宋时期数学家秦九韶(约1202 ~1261),给出了著名的秦九韶公式:

(3)一个三角形的三边长依次为![]() ,
,![]() ,
,![]() ,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x2+px﹣![]() )(x2﹣3x+q)的积中不含x项与x3项
)(x2﹣3x+q)的积中不含x项与x3项
(1)求p、q的值;
(2)求代数式(﹣2p2q)2+(3pq)0+p2019q2020的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有![]() 棵枇杷树.每棵平均产量为
棵枇杷树.每棵平均产量为![]() 千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量
千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量![]() 千克,若设增种
千克,若设增种![]() 棵枇杷树,投产后果园枇杷的总产量为
棵枇杷树,投产后果园枇杷的总产量为![]() 千克,则
千克,则![]() 与
与![]() 之间的函数关系式为________.
之间的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com