
【题目】综合与实践
问题情境
在学习了《勾股定理》和《实数》后,某班同学以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动.
操作发现
“毕达哥拉斯”小组的同学想到借助正方形网格解决问题.如图1是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C、A,他们借助此图求出了△ABC的面积.

(1)在图1中,所画的△ABC的三边长分别是AB= ,BC= ,AC= ; △ABC的面积为 .
实践探究
(2)在图2所示的正方形网格中画出△DEF(顶点都在格点上),使DE=![]() ,DF=
,DF=![]() , EF=
, EF=![]() ,并写出△DEF的面积.
,并写出△DEF的面积.
继续探究
“秦九韶”小组的同学想到借助曾经阅读的数学资料: 已知三角形的三边长分别为a、b、c,求其面积,对此问题中外数学家曾经进行过深入研究.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式:
![]()
我国南宋时期数学家秦九韶(约1202 ~1261),给出了著名的秦九韶公式:

(3)一个三角形的三边长依次为![]() ,
,![]() ,
,![]() ,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
科目:初中数学 来源: 题型:
【题目】“8字”的性质及应用:
(1)如图1,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
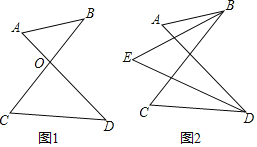
(2)如图2,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明:∠E=![]() (∠A+∠C).
(∠A+∠C).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形的中心在原点![]() ,且正方形的一组对边与
,且正方形的一组对边与![]() 轴平行.点
轴平行.点![]() 是反比例幽数
是反比例幽数![]() 的图象上与正方形的一个交点,若图中阴影部分的面积等于
的图象上与正方形的一个交点,若图中阴影部分的面积等于![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ﹙
﹙![]() ,
,![]() ﹚,
﹚,![]() ﹙
﹙![]() ,
,![]() ﹚,交
﹚,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.

![]() 求反比例函数
求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
![]() 连接
连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
![]() 根据图象写出使一次函数的值小于反比例函数的值的
根据图象写出使一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
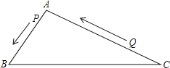
【题目】如图,![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 厘米的速度向
厘米的速度向![]() 运动,点
运动,点![]() 从
从![]() 同时出发,以每秒
同时出发,以每秒![]() 厘米的速度向
厘米的速度向![]() 运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以
运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,运动时间为________.
相似时,运动时间为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在一次高尔夫球争霸赛中从山坡上的点![]() 打出一球向球洞
打出一球向球洞![]() 飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度
飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度![]() 时,球移动的水平距离为
时,球移动的水平距离为![]() .已知山坡
.已知山坡![]() 与水平方向
与水平方向![]() 的夹角为
的夹角为![]() ,
,![]() ,
,![]() 两点相距
两点相距![]()
![]() .
.
![]() 求出点
求出点![]() 的坐标;
的坐标;
![]() 求抛物线解析式.并判断小明这一杆能否把高尔夫球从点
求抛物线解析式.并判断小明这一杆能否把高尔夫球从点![]() 直接打入球洞
直接打入球洞![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在CD边上,将△ADE沿AE对折得到△AFE,延长EF交BC边于点G,连结AG.给出结论:①△ABG≌△AFG;②∠EAG=45°;③∠AGB+∠AED=135°.其中正确的结论有( )

A.只有①B.①②C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com