Question

【题目】“8字”的性质及应用：

（1）如图1，AD、BC相交于点O，得到一个“8字”ABCD，求证：∠A+∠B＝∠C+∠D．

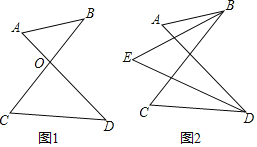
（2）如图2，∠ABC和∠ADC的平分线相交于点E，利用（1）中的结论证明：∠E＝（∠A+∠C）．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）根据三角形的内角和定理和对顶角相等即可证∠A+∠B＝∠C+∠D；

（2）根据角平分线的定义可得：∠ABE=∠EBC，∠CDE=∠EDA，再根据（1）中结论列出两个等式，将两个等式相加即可证出∠E＝（∠A+∠C）．

证明：（1）∵∠A+∠B=180°－∠AOB，∠C+∠D=180°－∠COD，∠AOB=∠COD，

∴∠A+∠B＝∠C+∠D；

（2）∵∠ABC和∠ADC的平分线相交于点E，

∴∠ABE=∠EBC，∠CDE=∠EDA，

由（1）的结论可知：∠A＋∠ABE=∠E＋∠EDA①，∠C＋∠CDE=∠E＋∠EBC②，

①＋②得：∠A＋∠ABE＋∠C＋∠CDE=∠E＋∠EDA＋∠E＋∠EBC，

∴∠A＋∠C=2∠E，

∴∠E＝（∠A+∠C）.