
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

【答案】(1)见解析;(2)70°.
【解析】
(1)根据全等三角形的判定即可判断△AEC≌△BED;
(2)由(1)可知:EC=ED,∠C=∠BDE,根据等腰三角形的性质即可知∠C的度数,从而可求出∠BDE的度数.
证明:(1)∵AE和BD相交于点O,∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,∴∠1=∠BEO,∴∠AEC=∠BED.
在△AEC和△BED中,
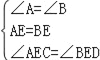
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,∵EC=ED,∠1=40°,∴∠C=∠EDC=70°,
∴∠BDE=∠C=70°.


科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉,例如:|6+7|=6+7;|7﹣6|=7﹣6;|6﹣7|=7﹣6;|﹣6﹣7|=6+7.
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:
①|7+21|=______;②|﹣![]() +0.8|=______;③
+0.8|=______;③![]() =______;
=______;
(2)用合理的方法进行简便计算:![]()
(3)用简单的方法计算:|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |+…+|
|+…+|![]() ﹣
﹣![]() |.
|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习多项式乘以多项式时发现:(![]() x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:![]() x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(![]() x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
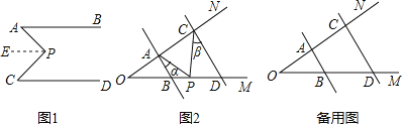
【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有小莉,小罗,小强三个自愿献血者,两人血型为O型,一人血型为A型.若在三人中随意挑选一人献血,两年以后又从此三人中随意挑选一人献血,试求两次所抽血的血型均为O型的概率.(要求:用列表或画树状图的方法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com