

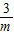 ��0�����۲�ͼ����������������ABCΪRt��ʱ����֪��AOC�ס�COB���������OB�ij��ȣ�����ABCΪ���������ʱ����0��
��0�����۲�ͼ����������������ABCΪRt��ʱ����֪��AOC�ס�COB���������OB�ij��ȣ�����ABCΪ���������ʱ����0��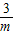 ��9�����m��ȡֵ��Χ���ɣ�
��9�����m��ȡֵ��Χ���ɣ�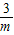 ����3�֣�
����3�֣�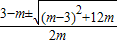 =
=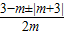 ��
��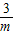 ��
��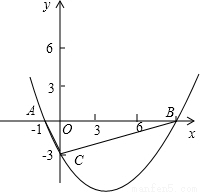 �ڣ�I����m��0ʱ���ɢٿ�֪�����߿������ϣ��ҹ���A��-1��0����C��0��-3����B��
�ڣ�I����m��0ʱ���ɢٿ�֪�����߿������ϣ��ҹ���A��-1��0����C��0��-3����B��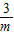 ��0����
��0����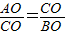 ��
��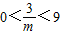 ������m��
������m�� ��
�� ʱ����ABCΪ��������Σ�
ʱ����ABCΪ��������Σ�  ʱ����ABCΪ��������Σ�
ʱ����ABCΪ��������Σ�

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
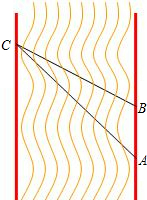 ��һ����ѧ����ϣ���ʦ����ѧ��ȥ��һ���ϱ�����ĺӿ�����ͼ��ʾ��ijѧ���ںӶ�����A���۲�Ӷ�ˮ����һ��C�����C��A��ƫ��31��ķ����ϣ��غӰ���ǰ��20����B�������C��B��ƫ��45��ķ����ϣ���������������ݣ�������ͬѧ����������ӵĿ��ȣ����ο���ֵ��tan31���
��һ����ѧ����ϣ���ʦ����ѧ��ȥ��һ���ϱ�����ĺӿ�����ͼ��ʾ��ijѧ���ںӶ�����A���۲�Ӷ�ˮ����һ��C�����C��A��ƫ��31��ķ����ϣ��غӰ���ǰ��20����B�������C��B��ƫ��45��ķ����ϣ���������������ݣ�������ͬѧ����������ӵĿ��ȣ����ο���ֵ��tan31���| 3 |
| 5 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
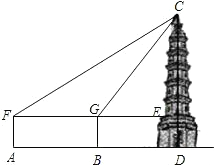 ʱ������ǡ�CGE=37�㣬��֪��������1.5�ף���������������ݼ��������CD�ĸ߶ȣ�
ʱ������ǡ�CGE=37�㣬��֪��������1.5�ף���������������ݼ��������CD�ĸ߶ȣ�| 3 |
| 5 |
| 3 |
| 4 |
| 9 |
| 25 |
| 3 |
| 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
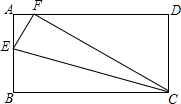 ��һ����ѧ����ϣ�����ͬѧ������ABCD��ֱ��CE�۵�������Bǡ������AD����F�㴦����ͼ��ʾ����֪CD=8cm��BE=5cm����AD=
��һ����ѧ����ϣ�����ͬѧ������ABCD��ֱ��CE�۵�������Bǡ������AD����F�㴦����ͼ��ʾ����֪CD=8cm��BE=5cm����AD=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��һ����ѧ����ϣ���ʦ����ѧ��ȥ�ⳤ���Ŀ��ȣ�ijѧ���ڳ���������A���۲������ˮ����һ��C�����C��A���Ϸ����ϣ��س�������ǰ��200����B�������C��B��ƫ��30��ķ����ϣ�
��һ����ѧ����ϣ���ʦ����ѧ��ȥ�ⳤ���Ŀ��ȣ�ijѧ���ڳ���������A���۲������ˮ����һ��C�����C��A���Ϸ����ϣ��س�������ǰ��200����B�������C��B��ƫ��30��ķ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��һ����ѧ����ϣ�����ʦ��ѧ������һ�鳤40cm����30cm�ij�����ֽƬ����ͼ����Ҫ���۳�һ����Ϊ5cm���ǵ����ݻ����ij�������ӣ�
��һ����ѧ����ϣ�����ʦ��ѧ������һ�鳤40cm����30cm�ij�����ֽƬ����ͼ����Ҫ���۳�һ����Ϊ5cm���ǵ����ݻ����ij�������ӣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com