
【题目】如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.
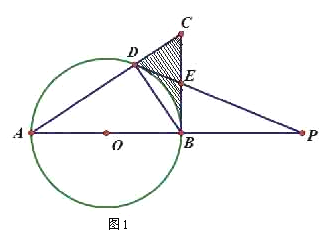

(1)求证:PD是⊙O的切线;
(2)若BD=BP=2![]() ,求图中曲边三角形(阴影部分)的周长;
,求图中曲边三角形(阴影部分)的周长;
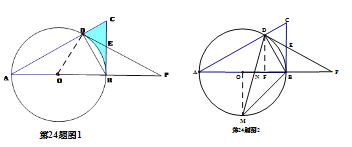
(3)如图2,点M是![]() 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A=![]() ,求
,求![]() 的值.
的值.
【答案】(1)、证明过程见解析;(2)、6+![]() ;(3)、
;(3)、![]() .
.
【解析】
试题分析:(1)、连接OD,根据直径得出∠ADB=90°,根据OA=OB得∠A+∠ABD=90°,根据OA=OB=OD得出∠ADO=∠A,则∠BDO=∠ABD,从而得到∠PDO=90°,说明切线;(2)、根据题意得出△BOD为正三角形,根据弧长计算公式求出弧BD的长度,根据Rt△BDC得出DC,BC的长度,然后计算曲边三角形的周长;(3)、连接OM,过D作DF⊥AB于F,根据点M为弧的中点可得OM⊥AB,设BD=x,则AD=2x,AB=![]() x,DF=
x,DF=![]() ,根据△OMN和△FDN相似得出答案.
,根据△OMN和△FDN相似得出答案.
试题解析:(1)、连结OD
∵AB是⊙O的直径
∴∠ADB=90°,OA=OB,∠A+∠ABD=90°
又∵OA=OB=OD
∴∠ADO=∠A
∴∠BDO=∠ABD
又∵∠A=∠PDB
∴∠PDB+∠BD0=90°
即∠PDO=90°且D在圆上
∴PD是⊙O的切线;
(2)、由已知和(1)可得,△ABD≌△POD,
易得△BOD为等边三角形,
∴∠ADB=∠ACB=60°,OA=OB=OD=BD
∴![]() =
=![]()
又在Rt△BDC中,∠ACB=60°,BD=![]()
∴DC=2,BC=4
∴曲边三角形(阴影部分)的周长为:![]()
(3)、连结OM,过D作DF⊥AB于F
∵点M是![]() 的中点, ∴OM⊥AB
的中点, ∴OM⊥AB
设BD=x,则AD=2x,AB=![]() ,DF=
,DF=![]()
由△OMN∽△FDN得


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们在日常生活中有许多行为动作:如①拉抽屉;②拧水龙头;③划小船;④调钟表;⑤推动推拉门;⑥转动方向盘;⑦乘电梯.我们用数学的眼光来看,其中属于旋转的有_______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在电脑中设置了一个有理数的运算程序:输入数a,加*键,在输入数b,就可以得到运算:a*b=(a-b)-|b-a|.
(1)求(-3)*2的值;
(2)求(3*4)*(-5)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某口袋中有红色、黄色、蓝色玻璃球共72个,小明通过多次摸球试验后,发现摸到红球、黄球、蓝球的频率为35%、25%和40%,估计口袋中黄色玻璃球有 个。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com