Question

【题目】如图1，已知A（，0），B（0， ）分别为两坐标轴上的点，且、满足，OC∶OA=1∶3．

（1）求A、B、C三点的坐标；

（2）若D（1，0），过点D的直线分别交AB、BC于E、F两点，设E、F两点的横坐标分别为．当BD平分△BEF的面积时，求的值；

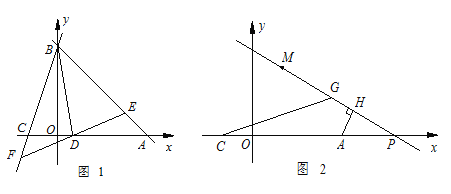
（3）如图2，若M（2，4），点P是轴上A点右侧一动点，AH⊥PM于点H，在HM上取点G，使HG=HA，连接CG，当点P在点A右侧运动时，∠CGM的度数是否改变？若不变，请求其值；若改变，请说明理由．

Answer 1

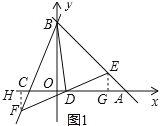
【答案】（1）A（6，0），B（0，6），C（－2，0）；（2）；（3）不改变．

【解析】试题分析：（1）由偶次方和算术平方根的非负性质求出a和b的值，得出点A、B的坐标，再求出OC，即可得出点C的坐标；

（2）作EG⊥x轴于G，FH⊥x轴于H，由三角形的面积关系得出DF=DE，由AAS证明△FDH≌△EDG，得出DH=DG，即可得出结果；

（3）作MQ⊥x轴于Q，连接CM、AG、M，证出△MCQ是等腰直角三角形，得出∠MCQ=45°，同理：△MPQ是等腰直角三角形，∠MAQ=45°，△AHG是等腰直角三角形，得出∠AGH=45°=∠MCQ，证出A、G、M、C四点共圆，由圆周角定理即可得出结论．

试题解析：（1）∵，

∴a-b=0，b-6=0，

∴a=b=6，

∴A（6，0），B（0，6），

∴OA==OB=6，

∵OC：OA=1：3，

∴OC=2，

∴C（－2，0）．

(2)作EG⊥x轴于G，FH⊥x轴于H，如图1所示：

则∠FHD=∠EGD=90°，

∵BD平分△BEF的面积，

∴DF=DE，

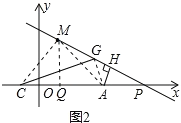
在△FDH和△EDG中， ，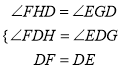

∴△FDH≌△EDG(AAS)，

∴DH=DG，即xE+1=xF1，

∴xE+xF=2；

（3）∠CGM的度数不改变，∠CGM=45°；

理由如下：作MQ⊥x轴于Q，连接CM、AG、M，如图2所示：

则MQ=4，OQ=2，

∴CQ=2+2=4，

∴△MCQ是等腰直角三角形，

∴∠MCQ=45°，

同理：△MQA是等腰直角三角形，

∴∠MAQ=45°，

∵AH⊥PM，HG=HA，

∴△AHG是等腰直角三角形，

∴∠AGH=45°=∠MCQ，

∴A、G、M、C四点共圆，

∴∠CGM=∠MAQ=45°.