
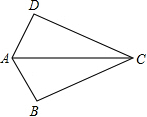
| A. | CB=CD | B. | AB=AD | C. | ∠BCA=∠DCA | D. | ∠B=∠D |
分析 全等三角形的判定定理有SAS,ASA,AAS,SSS,根据以上内容判断即可.
解答 解:A、根据CB=CD,AC=AC,∠BAC=∠DAC,不能推出△BAC和△DAC全等,故本选项符合题意;
B、∵在△ABC和△ADC中,AB=AD,∠BAC=∠DAC,AC=AC,
∴根据SAS可以判定△ABC≌△ADC,故本选项不符合题意;
C、∵在△ABC和△ADC中,∠BAC=∠DAC,AC=AC,∠BCA=∠DCA,
∴根据ASA可以判定△ABC≌△ADC,故本选项不符合题意;
D、∵在△ABC和△ADC中,∠B=∠D,∠BAC=∠DAC,AC=AC,
∴根据AAS可以判定△ABC≌△ADC,故本选项不符合题意.
故选:A.
点评 本题考查了全等三角形的判定,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
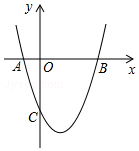 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
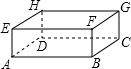 如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.
如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com