
���Ķ�����IJ��ϣ��ٷֽ���ʽ��
Ҫ�Ѷ���ʽam+an+bm+bn�ֽ���ʽ�������Ȱ�����ǰ����ֳ�һ�飬�����a�������ĺ�����ֳ�һ�飬�����b���Ӷ��õ�a��m+n��+b��m+n������ʱ������a��m+n��+b��m+n�����й���ʽ��m+n�������ǿ��ṫ��ʽ��m+n�����Ӷ��õ���m+n����a+b���������am+an+bm+bn=��am+an��+��bm+bn��=a��m+n��+b��m+n��=��m+n����a+b����
������ʽ�ֽ�ķ�����������ֽⷨ�������һ������ʽ������鲢�������ʽ�����ǵ���һ����ʽ������ͬ����ô�������ʽ�Ϳ������÷���ֽⷨ���ֽ���ʽ�ˣ�
��������������ṩ�ķ����ֽ���ʽ��
��1��a2��ab+ac��bc�� ��2��m2+5n��mn��5m��
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| (x1-x2)2+(y1-y2)2 |
| (x1-x2)2+(y1-y2)2 |
| 6 |
| 7 |
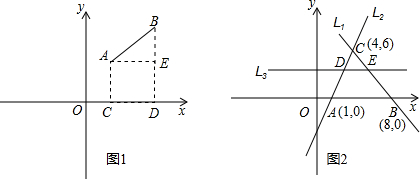
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 4+2 |
| 3 |
| 11+1 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ʮ�� ���ͣ������
| Q | W | E | R | T | Y | U | I | O | P | A | S | D |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| F | G | H | J | K | L | Z | X | C | V | B | N | M |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 4+2 |
| 3 |
| 11+1 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2003�����ʡʮ�����п���ѧ�Ծ��������棩 ���ͣ������
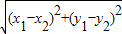 ������������֤�������ʽ��֤������ͼ1����A����X��Ĵ��ߣ�����ΪC����C��ĺ�����Ϊx1����B����X��Ĵ��ߣ�����ΪD����D��ĺ�����Ϊx2����A����BD�Ĵ��ߣ�����ΪE����E��ĺ�����Ϊx2��������Ϊy1����|AE|=|CD|=|x1-x2|
������������֤�������ʽ��֤������ͼ1����A����X��Ĵ��ߣ�����ΪC����C��ĺ�����Ϊx1����B����X��Ĵ��ߣ�����ΪD����D��ĺ�����Ϊx2����A����BD�Ĵ��ߣ�����ΪE����E��ĺ�����Ϊx2��������Ϊy1����|AE|=|CD|=|x1-x2|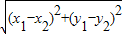 ����Ϊ|AB|��ʾ�߶γ���Ϊ�Ǹ�����
����Ϊ|AB|��ʾ�߶γ���Ϊ�Ǹ����� �����߶�|DA|�ij���
�����߶�|DA|�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com