
����Ŀ���������������
��1��һ������ӵ�������10��������Ҷӵ�������15�������������5������ס��Һ���������µĹ����������Ӻ��������������������
��2����A�ص�B����������10Сʱ����B�ص�A����������15Сʱ���ס������˴�A��B��������������׳���5Сʱ���ҳ��������ҳ�����Сʱ������������
��3��һ��Ǯ���������������Ʒ10������������Ʒ15���������Ǯ�����˼ס���������Ʒ����֪������Ʒ��������Ʒ������5������������Ʒ���˼�����
��4��ͨ��������������������㷢����ʲô��
��5�������������еķ�������дһ��ʵ�������Ӧ������
���𰸡���1��3����2��3����3��3����4���𰸼���������5���𰸼�����.
��������
��1������Һ���x����ɣ����ݼ����ù��������������֣�+�����ù�����=�ܹ�����1�г����̣��ⷽ�̼����������2��������������ľ���Ϊ����1���ҳ���xСʱ���������������ݼ��ߵ�·�̣��������֣�+���ߵ�·��=��·��1�з��̣��ⷽ�̼�����⣻��3���蹺��������Ʒx������Ǯ��Ϊ����1�����ݹ������Ʒ��Ǯ��+��������Ʒ��Ǯ��=��Ǯ��1�г��������ⷽ�̼�����⣻��4������ǰ���ʿɵó���������������ݲ�һ���⣬������ϵ��һ�µ�����5���������̼��ɣ�
��1������Һ���x����ɣ���![]() ��
��
��֮�ã�x=3��
�����Ӻ���3�������������.
��2��������������ľ���Ϊ����1���ҳ���xСʱ������������![]() ��
��
��֮����x=3��
���ҳ���3Сʱ����������.
��3���蹺��������Ʒx������Ǯ��Ϊ����1��
��![]() ��
��
��֮�ã�x=3��
��������Ʒ����3��.
��4����������������ݲ�һ���⣬������ϵ��һ�µģ�
��5����ʦ�ڵ��ˣ�ѧ���������ð�Ѹ��ον�ʦ�������Ʒ���������飬�������Ǯ�����ˮ��10��������ˮ��15���������Ǯ�����˼ס�������ˮ������֪����ˮ��������ˮ��������5����������ˮ�����˼�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��k��0����ͼ���뷴�������� ![]() ��ͼ���ڶ��������ڵ�A��B ���㣬��x�ύ��C�㣬��B������Ϊ��6��n�����߶�OA=5��EΪx�Ḻ������һ�㣬��sin��AOE=
��ͼ���ڶ��������ڵ�A��B ���㣬��x�ύ��C�㣬��B������Ϊ��6��n�����߶�OA=5��EΪx�Ḻ������һ�㣬��sin��AOE= ![]() ��
�� 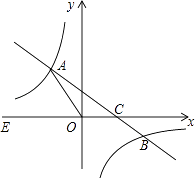
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����AOC�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵʱ�Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ��ȤС����һ����ѧ�����У��������У10��ͬѧ�μӽ������ѧҵˮƽ���Ե������ɼ����õ�������±���ʾ��

����˵����ȷ���ǣ� ��
A����10��ͬѧ�����ɼ�����λ��Ϊ38��
B����10��ͬѧ�����ɼ���ƽ����Ϊ38��
C����10��ͬѧ�����ɼ�������Ϊ39��
D����10��ͬѧ�����ɼ��ķ���Ϊ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ��11����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������29�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮

�ʣ���1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵǰ�갴�ɻ�������������15Ԫ/�֡����ɻ�������������25Ԫ/�ֵ��շѱ�����֧����������������5000Ԫ����ȥ��Ԫ�����շѱ��ϵ�Ϊ���ɻ�������������30Ԫ/�֣����ɻ�������������100Ԫ/�֣�������ҵȥ�괦��������������������ǰ�����û�б仯�������ۺ��Ҫ��֧��������9000Ԫ��
��1������ҵǰ�괦���Ŀɻ��������Ͳ��ɻ������������ٶ֣�
��2������ҵ�ƻ����꽫�����������������������ٵ�200�֣��ҿɻ������������ڲ��ɻ���������������3������������ҵ�����ж��ٶֿɻ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ��![]() ��1�IJ������£�
��1�IJ������£�
����������һ����![]() ��1�������Ļ������ʣ�
��1�������Ļ������ʣ�
�ڶ�����2x��1��3��2x+8����3�������٣�
��������2x��1��6x+24��3�������ڣ�
���IJ���2x��6x��24��3+1�������ۣ�
���岽����4x��22���ܣ�
��������x����![]() �������ݣ�
�������ݣ�
���Ͻⷽ�̵ڶ������������ļ��������У���ȥ���ŷ�������ʽ����һ������ʽ���ʶ������ϲ�ͬ�������ѡ��������ȫ��ȷ��һ��ѡ�������
A. �ڢ٢ۢܢ� B. �ڢ٢ۢܢ� C. �ۢ٢ڢܢ� D. �ۢ٢ܢڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��

��1����֤��OE=OF��
��2����CE=12��CF=5����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��A��B��C������ֱ�ΪA�� ![]() ��0����B��3
��0����B��3 ![]() ��0����C��0��5������D�ڵ�һ�����ڣ��ҡ�ADB=60�㣬���߶�CD�ij�����Сֵ�ǣ� ��
��0����C��0��5������D�ڵ�һ�����ڣ��ҡ�ADB=60�㣬���߶�CD�ij�����Сֵ�ǣ� ��
A.2 ![]() ��2
��2
B.2 ![]()
C.2 ![]()
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AE��BC�ڵ�E���ӳ�BC����FʹCF��BE������AF��DE��DF.
(1)��֤���ı���AEFD�Ǿ��Σ�
(2)��AB��6��DE��8��BF��10����AE�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com