
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先证明四边形AEFD是平行四边形,再证明∠AEF=90°即可.
(2)证明△ABF是直角三角形,由三角形的面积即可得出AE的长.
试题解析:(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即EF=BC.
∵在ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.
∵AE⊥BF,
∴△ABF的面积=![]() ABAF=
ABAF=![]() BFAE.
BFAE.
∴AE=![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】阅读填空,并完成问题:“绝对值”一节学习后,数学老师对同学们的学习进行了拓展.数学老师向同学们提出了这样的问题:“在数轴上,一个数的绝对值就是表示这个数的点到原点的距离.那么,如果用P(a)表示数轴上的点P表示有理数a,Q(b)表示数轴上的点Q表示有理数b,那么点P与点Q的距离是多少?”
(1)聪明的小明经过思考回答说:这个问题应该有两种情况.一种是点P和点Q在原点的两侧,此时点P与点Q的距离是a和b的绝对值的和,即∣a∣+∣b∣.例如:点A(-3)与点B(5)的距离为∣-3∣+∣-5∣= ;
另一种是点P和点Q在原点的同侧,此时点P与点Q的距离的a和b中,较大的绝对值减去较小的绝对值,即∣a∣-∣b∣或∣b∣-∣a∣.例如:点A(-3)与点B(-5)的距离为∣-5∣-∣-3∣= ;
你认为小明的说法有道理吗?如果没有道理,请你指出错误之处;如果有道理,请你模仿求出数轴上点M(![]() )与N(
)与N(![]() )之间和点C(-2)与D(-7)之间的距离.
)之间和点C(-2)与D(-7)之间的距离.
(2)小颖在听了小明的方法后,提出了不同的方法,小颖说:我们可以不考虑点P和点Q所在的位置,无论点P与点Q的位置如何,它们之间的距离就是数a与b的差的绝对值,即∣a-b∣.例如:点A(-3)与点B(5)的距离就是∣-3-5∣= ;点A(-3)与点B(-5)的距离就是∣(-3)-(-5)∣= ;你认为小颖的说法有道理吗?如果没有道理,请你指出错误之处;如果有道理,请你模仿求出数轴上点M(![]() )与N(
)与N(![]() )之间和点C(-1.5)与D(-3.5)之间的距离.
)之间和点C(-1.5)与D(-3.5)之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号)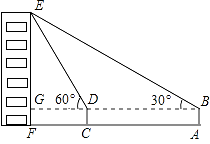
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.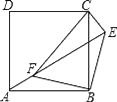
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]() (
( ![]() <
< ![]() <0)与x轴最多有一个交点,现有以下结论:
<0)与x轴最多有一个交点,现有以下结论:
① ![]() <0;②该抛物线的对称轴在y轴左侧;③关于x的方程
<0;②该抛物线的对称轴在y轴左侧;③关于x的方程 ![]() 有实数根;④对于自变量x的任意一个取值,都有
有实数根;④对于自变量x的任意一个取值,都有 ![]() ,其中正确的为( )
,其中正确的为( )
A.①②
B.①②④
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B在数轴上表示的数分别是m,n.
(1)填写下表:

(2)若A,B两点间的距离为d,写出d与m,n之间的数量关系.
(3)在数轴上标出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求出所有这些整数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
求证:四边形CDC′E是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的有理数为a,将点A向左移动6个单位长度,再向右移动2个单位长度与点B重合,点B对应的有理数为﹣24.
(1)求a;
(2)如果数轴上的点C在数轴上移动3个单位长度后,距B点8个单位长度,那么移动前的点C距离原点有几个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com