
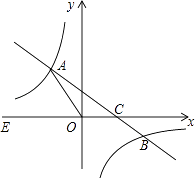
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 ![]() 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=
的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= ![]() .
. 
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数值时自变量x的取值范围.
【答案】
(1)解:作AD⊥x轴于D,如图,
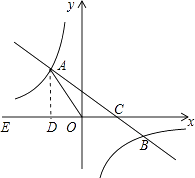
在Rt△OAD中,∵sin∠AOD= ![]() =
= ![]() ,
,
∴AD= ![]() OA=4,
OA=4,
∴OD= ![]() =3,
=3,
∴A(﹣3,4),
把A(﹣3,4)代入y= ![]() 得m=﹣4×3=﹣12,
得m=﹣4×3=﹣12,
所以反比例函数解析式为y=﹣ ![]() ;
;
把B(6,n)代入y=﹣ ![]() 得6n=﹣12,解得n=﹣2,
得6n=﹣12,解得n=﹣2,
把A(﹣3,4)、B(6,﹣2)分别代入y=kx+b得 ![]() ,解得
,解得 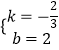 ,
,
所以一次函数解析式为y=﹣ ![]() x+2
x+2
(2)解:当y=0时,﹣ ![]() x+2=0,解得x=3,则C(3,0),
x+2=0,解得x=3,则C(3,0),
所以S△AOC= ![]() ×4×3=6
×4×3=6
(3)解:当x<﹣3或0<x<6时,一次函数的值大于反比例函数的值
【解析】(1)作AD⊥x轴于D,如图,先利用解直角三角形确定A(﹣3,4),再把A点坐标代入y= ![]() 可求得m=﹣12,则可得到反比例函数解析式;接着把B(6,n)代入反比例函数解析式求出n,然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组,再解方程组求出a和b的值,从而可确定一次函数解析式;(2)先确定C点坐标,然后根据三角形面积公式求解;(3)观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
可求得m=﹣12,则可得到反比例函数解析式;接着把B(6,n)代入反比例函数解析式求出n,然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组,再解方程组求出a和b的值,从而可确定一次函数解析式;(2)先确定C点坐标,然后根据三角形面积公式求解;(3)观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】①在数轴上没有点能表示![]() +1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是
+1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是![]() =±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______.
=±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为 时,△ABE与以D、M、N为顶点的三角形相似.( ) 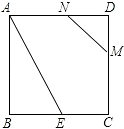
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
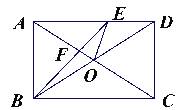
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国际无烟日”之际,小敏同学就一批公众对在餐厅吸烟所持的三种态度(彻底禁烟、建立吸烟室、其他)进行了调查,并把调查结果绘制成如图①,②的统计图.请根据下面图中的信息回答下列问题:
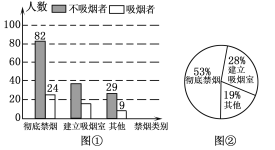
(1)被调查者中,不吸烟者中赞成彻底禁烟的人数有________人;
(2)本次抽样调查的样本容量为__________;
(3)被调查者中,希望建立吸烟室的人数有_________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒). 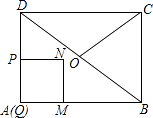
(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图,点A、B在数轴上分别表示有理数a、b,则A、B两点之间的距离可以表示为|a﹣b|.
根据阅读材料与你的理解回答下列问题:
(1)数轴上表示3与﹣2的两点之间的距离是 .
(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为 .
(3)代数式|x+8|可以表示数轴上有理数x与有理数 所对应的两点之间的距离;若|x+8|=5,则x= .
(4)求代数式|x+1008|+|x+504|+|x﹣1007|的最小值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
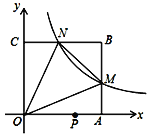
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() 分别相交于
分别相交于![]() 两点,
两点,![]() 的面积为10.若动点
的面积为10.若动点![]() 在
在![]() 轴上,则
轴上,则![]() 的最小值是_____________
的最小值是_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)一项工程,甲队单独做需10天完成,乙队单独做需15天完成,甲先做5天后,甲、乙合作完成余下的工作,问两队合做几天可以完成这项工作?
(2)从A地到B地,甲需走10小时,从B地到A地,乙需走15小时,甲、乙两人从A,B两地相向而行,甲出发5小时后乙出发,问乙出发几小时后两人相遇?
(3)一笔钱款,可以买甲种商品10件或买乙种商品15件,用这笔钱款买了甲、乙两种商品,已知甲种商品比乙种商品多买了5件,问乙种商品买了几件?
(4)通过解答上面三个问题,你发现了什么?
(5)根据上面所列的方程,编写一道实际问题的应用题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com