【题目】如图，将正方形纸片
折叠，使点
落在边
上的
处，点
落在
处，若
，则
的度数为（ ）
A. 100°B. 110°C. 120°D. 130°
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】某学校为了增强学生体质，决定开设以下体育课外活动项目：A．篮球 B．乒乓球C．羽毛球 D．足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，
请回答下列问题：
（1）这次被调查的学生共有多少人？
（2）请你将条形统计图（2）补充完整；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）
查看答案和解析>>
科目：初中数学 来源： 题型：
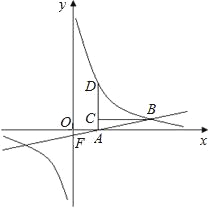
【题目】如图，点D在双曲线上，AD垂直x轴，垂足为A，点C在AD上，CB平行于x轴交双曲线于点B，直线AB与y轴交于点F，已知AC：AD=1：3，点C的坐标为（3，2）．
（1）求该双曲线的解析式；
（2）求△OFA的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，解答后面的问题：
材料：求代数式x2－2x＋5的最小值．
小明同学的解答过程：x2－2x＋5＝x2－2x＋1－1＋5＝(x－1)2＋4
我们把这种解决问题的方法叫做“配方法”．
(1)请按照小明的解题思路，写出完整的解答过程；
(2)请运用“配方法”解决问题：
①若x2＋y2－6x＋10y＋34＝0，求y－x的立方根；
②分解因式：4x4＋1．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A(－4，n)、B(3，4)是一次函数y1＝kx＋b的图象与反比例函数
的图象的两个交点，过点D(t，0)（0＜t＜3）作x轴的垂线，分别交双曲线
和直线y1＝kx＋b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时，S△BPQ＝
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN，试说明：边QM与双曲线
（x＞0）始终有交点
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的对角线AC，BD相交于点O，E是AC上的一点，且AB=AE，过点A作AF⊥BE，垂足为F，交BD于点G.点H在AD上，且EH∥AF.若正方形ABCD的边长为2，下列结论：①OE=OG；②EH=BE；③AH=
，其中正确的有（ ）
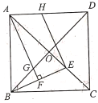
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点D、E分别是等边三角形ABC的边BC、AC上的点，连接AD、BE交于点O，且△ABD≌△BCE．
（1）若AB=3，AE=2，则BD= ；
（2）若∠CBE=15°，则∠AOE= ；
（3）若∠BAD=a，猜想∠AOE的度数，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，
，
，
，
，
，
，按照
的顺序，分别将这六个点的横、纵坐标依次循环排列下去，形成一组数1，1，-1，2，2，3，-2，4，3，5，-3，6，1，1，-1，2，…，第一个数记为
，第二个数记为
，…，第
个数记为
（为正整数），那么
和
的值分别为（ ）
A. 0，3B. 0，2C. 6，3D. 6，2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A，B分别在x轴、y轴上，点D在第一象限内，DC⊥x轴于点C，AO＝DC＝2，AB＝DA＝
，反比例函数y＝
(k＞0)的图象过CD的中点E.
(1)求证：△AOB≌△DCA；
(2)求k的值；
(3)△BFG和△DCA关于某点成中心对称，其中点F在y轴上，试判断点G是否在反比例函数的图象上，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
