
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,且AB=AE,过点A作AF⊥BE,垂足为F,交BD于点G.点H在AD上,且EH∥AF.若正方形ABCD的边长为2,下列结论:①OE=OG;②EH=BE;③AH=![]() ,其中正确的有( )
,其中正确的有( )
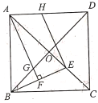
A. 0个B. 1个C. 2个D. 3个
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ;那么
;那么![]() 与
与![]() 平行吗?试说明理由.
平行吗?试说明理由.

请将下面的推理过程补充完整.
解:![]() ,理由如下:
,理由如下:
![]() (已知)
(已知)
![]() (平角的定义)
(平角的定义)
![]() ( )
( )
![]()
![]() ( )
( )
![]() (两直线平行,同位角相等)
(两直线平行,同位角相等)
![]() (已知)
(已知)
![]() ( )
( )
![]() (内错角相等,两直线平行)
(内错角相等,两直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).

(1) 上述操作能验证的等式是__________________;
(2) 应用你从(1)得出的等式,完成下列各题:
①已知x24y2=12,x+2y=4,求x2y的值.
②计算:(1![]() )(1
)(1![]() )(1
)(1![]() )…(1
)…(1![]() )(1
)(1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
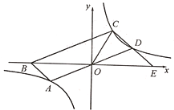
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AD经过O点,A、C、D三点都在反比例函数![]() 的图像上,B点在
的图像上,B点在![]() 轴的负半轴上,延长CD交
轴的负半轴上,延长CD交![]() 轴于点E,连接CO.
轴于点E,连接CO.
若C(1,2),D(2,1),则![]() 为_______.
为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
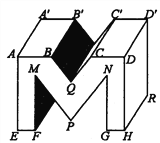
【题目】如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系?CC′与DH有何位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
2019年4月底,“百年器象——清华大学科学博物馆筹备展”上展出了一件清华校友捐赠的历史文物“Husun型六分仪”(图①),它见证了中国人民解放军海军的发展历程.六分仪是测量天体高度的手提式光学仪器,它的主要原理是几何光学中的反射定律.观察测者手持六分仪(图②)按照一定的观测步骤(图③显示的是其中第6步)读出六分仪加油弧标尺上的刻度,再经过一定计算得出观察测点的地理坐标.

请大家证明在使用六分仪测量时用到的一个重要结论(两次反射原理).
已知:在图④所示的“六分仪原理图”中,所观测星体记为![]() ,两个反射镜面位于
,两个反射镜面位于![]() 两处,
两处,![]() 处的镜面的在直线
处的镜面的在直线![]() 自动与
自动与![]() 刻度线
刻度线![]() 保持平行(即
保持平行(即![]() ),并与
),并与![]() 处的镜面所在直线
处的镜面所在直线![]() 交于点
交于点![]() ,
,![]() 所在直线与水平线
所在直线与水平线![]() 交于点
交于点![]() ,六分仪上刻度线
,六分仪上刻度线![]() 与
与![]() 刻度线的夹角
刻度线的夹角![]() ,观测角为
,观测角为![]() .(请注意小贴士中的信息)
.(请注意小贴士中的信息)
求证:![]()

请在答题卡上完成对紫结论的以下填空及后续证明过程(后续证明无需标注理由).
证明:∵![]()
∴![]() ( )
( )
∵![]()
∴![]() ( )
( )
∵![]() ( )
( )
又∵![]() (小贴士已知),
(小贴士已知),
∴![]() .
.
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ( ).
( ).
即![]() .
.
补全证明过程:(请在答题卡上完成)
查看答案和解析>>
科目:初中数学 来源: 题型:
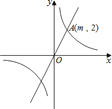
【题目】如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数![]() 的图象有一个交点A(m,2).
的图象有一个交点A(m,2).
(1)求m的值及正比例函数y=kx的解析式;
(2)试判断点B(2,3)是否在正比例函数图象上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com