
【题目】毕节市为加快新农村建设,建设美丽乡村,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金270万元;织金县建设了2个A类村庄和5个B类村庄共投入资金1020万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)黔西县改建3个A类美丽村庄和6个B类美丽村庄共需资金多少万元?
【答案】(1)建设一个A类美丽村庄所需资金是110万元,建设一个B类美丽村庄所需资金160万元.(2)黔西县改建3个A类美丽村庄和6个B类美丽村庄共需资金1290万元.
【解析】
(1)设建设一个A类美丽村庄所需资金是x万元,建设一个B类美丽村庄所需资金y万元,根据“建设一个A类美丽村庄和一个B类美丽村庄共需资金270万元;织金县建设了2个A类村庄和5个B类村庄共投入资金1020万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据总价=单价×数量,即可求出改建3个A类美丽村庄和6个B类美丽村庄所需费用.
(1)设建设一个A类美丽村庄所需资金是x万元,建设一个B类美丽村庄所需资金y万元,依题意,
得:![]() ,
,
解得:![]() ,
,
答:建设一个A类美丽村庄所需资金是110万元,建设一个B类美丽村庄所需资金160万元;
(2)110×3+160×6=1290(万元),
答:黔西县改建3个A类美丽村庄和6个B类美丽村庄共需资金1290万元.


科目:初中数学 来源: 题型:
【题目】从2020年开始,我市中考总分中要加大体育分值,某校为适应新的中考要求,决定为体育组添置一批体育器材.学校准备在网上订购一批某品牌足球和跳绳,在查阅天猫网店后发现足球每个定价140元,跳绳每条定价30元.现有![]() 、
、![]() 两家网店均提供包邮服务,并提出了各自的优惠方案.
两家网店均提供包邮服务,并提出了各自的优惠方案.
![]() 网店:买一个足球送一条跳绳;
网店:买一个足球送一条跳绳;
![]() 网店:足球和跳绳都按定价的90%付款.
网店:足球和跳绳都按定价的90%付款.
已知要购买足球60个,跳绳![]() 条(
条(![]() )
)
(1)若在![]() 网店购买,需付款 元(用含
网店购买,需付款 元(用含![]() 的代数式表示);若在
的代数式表示);若在![]() 网店购买,需付款 元(用含
网店购买,需付款 元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() 时,通过计算说明此时在哪家网店购买较为合算?
时,通过计算说明此时在哪家网店购买较为合算?
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
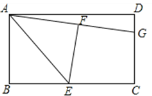
【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A.4n厘米B.4m厘米C.2(m+n)厘米D.4(m+n)厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC.
(1)求证:△BDG≌△ADC.
(2)分别取BG、AC的中点E、F,连接DE、DF,则DE与DF有何关系,并说明理由.
(3)在(2)的条件下,连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
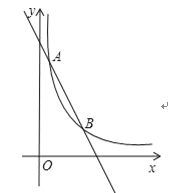
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若∠BEC=30°,求证:以BC,BE,AC边的三角形为直角三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com