
【题目】直线![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点B,与反比例函数
轴交于点B,与反比例函数![]() 的图象在第一象限交于点A,连接OA,若
的图象在第一象限交于点A,连接OA,若![]() ,则k的值为_____.
,则k的值为_____.
【答案】3
【解析】分析:先由直线y=x-2与y轴交于点C,与x轴交于点B,求出C(0,-2),B(2,0),由S△BOC=![]() OBOC,求出△BOC的面积,根据S△AOB:S△BOC=1:2,得出S△AOB的面积,求出yA=1,再把y=1代入y=x-2,解得x的值,得到A点坐标,然后将A点坐标代入y=
OBOC,求出△BOC的面积,根据S△AOB:S△BOC=1:2,得出S△AOB的面积,求出yA=1,再把y=1代入y=x-2,解得x的值,得到A点坐标,然后将A点坐标代入y=![]() ,即可求出k的值.
,即可求出k的值.
详解:∵直线y=x-2与y轴交于点C,与x轴交于点B,
∴C(0,-2),B(2,0),
∴S△BOC=![]() OBOC=
OBOC=![]() ×2×2=2,
×2×2=2,
∵S△AOB:S△BOC=1:2,
∴S△AOB=![]() S△BOC=1,
S△BOC=1,
∴![]() ×2×yA=1,
×2×yA=1,
∴yA=1,
把y=1代入y=x-2,
得1=x-2,解得x=3,
∴A(3,1).
∵反比例函数y=![]() 的图象过点A,
的图象过点A,
∴k=3×1=3.
故答案为:3.



科目:初中数学 来源: 题型:
【题目】(概念学习)
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,一般地,把![]() (a≠0)记作a,读作“a的圈n次方”.
(a≠0)记作a,读作“a的圈n次方”.
(初步探究)
(1)直接写出计算结果:2③=_____,(﹣![]() )⑤=_____.
)⑤=_____.
(2)关于除方,下列说法准确的选项有_________(只需填入正确的序号)
①.任何非零数的圈2次方都等于1; ②.对于任何正整数n,1=1;
③.3④=4③ ④.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
例如: 2④=2÷2÷2÷2
=2×![]() ×
×![]() ×
×![]()
=(__)2 (幂的形式)
试一试:将下列除方运算直接写成幂的形式.
5⑥=_____;(﹣![]() )⑩=_____;a=_____(a≠0).
)⑩=_____;a=_____(a≠0).
算一算:![]() ④÷23+(﹣8)×2③.
④÷23+(﹣8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,按如图所示有序排列.
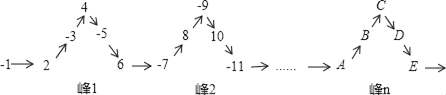
如图所示有序排列.如:“峰1”中峰顶C的位置是有理数4,那么,
(1)“峰6”中峰顶C的位置是有理数_____;
(2)2008应排在A、B、C、D、E中_____的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC=![]() .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毕节市为加快新农村建设,建设美丽乡村,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金270万元;织金县建设了2个A类村庄和5个B类村庄共投入资金1020万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)黔西县改建3个A类美丽村庄和6个B类美丽村庄共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,OM和ON分别平分∠AOC和∠BOC.
(1)如图:若C为∠AOB内一点,探究∠MON与∠AOB的数量关系;
(2)若C为∠AOB外一点,且C不在OA、OB的反向延长线上,请你画出图形,并探究∠MON与∠AOB的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式M=(a+b+1)x3+(2a﹣b)x2+(a+2b)x﹣4是关于x的二次多项式.
(1)若方程3(a+b)y=ky﹣8的解是y=4,求k的值;
(2)当x=2时,代数式M的值为﹣34.当x=﹣2时,求代数式M的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出总的销售利润y元与销售单价提高x元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com