
【题目】已知,OM和ON分别平分∠AOC和∠BOC.
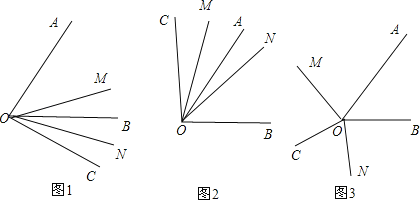
(1)如图:若C为∠AOB内一点,探究∠MON与∠AOB的数量关系;
(2)若C为∠AOB外一点,且C不在OA、OB的反向延长线上,请你画出图形,并探究∠MON与∠AOB的数量关系.

【答案】(1)∠MON=![]() ∠AOB;(2)∠MON=
∠AOB;(2)∠MON=![]() ∠AOB,或∠MON=180°﹣
∠AOB,或∠MON=180°﹣![]() ∠AOB.
∠AOB.
【解析】
(1)根据角平分线的性质利用等量代换求出∠MON与∠AOB的数量关系(2)利用角平分线的性质结合分类思想分别画图探究∠MON与∠AOB的数量关系.
解:(1)∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,
∠BOC,
∴∠MOC+∠NOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() ∠AOB,
∠AOB,
即∠MON=![]() ∠AOB;
∠AOB;
(2)如图1,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,
∠BOC,
∴∠MOC﹣∠NOC=![]() AOC﹣
AOC﹣![]() ∠BOC=
∠BOC=![]() ∠AOB,
∠AOB,
即∠MON=![]() ∠AOB;
∠AOB;
如图2,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,
∠BOC,
∴∠NOC﹣∠MOC=![]() ∠BOC﹣
∠BOC﹣![]() ∠AOC=
∠AOC=![]() ∠AOB,
∠AOB,
即∠MON=![]() ∠AOB;
∠AOB;
如图3,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,
∠BOC,
∴∠MOC+∠NOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (360°﹣∠AOB)
(360°﹣∠AOB)
即∠MON=180°﹣![]() ∠AOB.
∠AOB.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
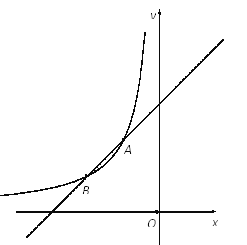
【题目】如图,函数![]() (x<0)与y=ax+b的图象交于点A(-1,n)和B(-2,1),直线y=mx与
(x<0)与y=ax+b的图象交于点A(-1,n)和B(-2,1),直线y=mx与![]() (x<0)的图象交于点P,与y=-x+1的图象交于点Q,定义∠PAQ为这个函数的“函数角”.
(x<0)的图象交于点P,与y=-x+1的图象交于点Q,定义∠PAQ为这个函数的“函数角”.
(1)求k,a,b的值;
(2)当m=-![]() 时,求这个函数的“函数角”的度数.
时,求这个函数的“函数角”的度数.
(3)若射线AP与x轴交于点N(a,0),当这个函数的“函数角”的度数不小于120°时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,……按照此规律继续下去,则S2019的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边CD的中点.
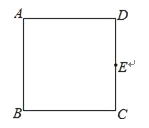
(1)用直尺和圆规作⊙O,使⊙O经过点A、B、E(保留作图痕迹,不写作法);
(2)若正方形ABCD的边长为2,求(1)中所作⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若任意一个三位数t的百位数字为a,十位数字为b,个位数字为c,那么可将这个三位数表示为t=![]() (a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(1)根据以上材料:F(258)= ;
(2)若一个三位数t=![]() ,且P(t)=0,F(t)=135,求这个三位数.
,且P(t)=0,F(t)=135,求这个三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
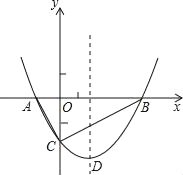
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com