
【题目】若任意一个三位数t的百位数字为a,十位数字为b,个位数字为c,那么可将这个三位数表示为t=![]() (a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(1)根据以上材料:F(258)= ;
(2)若一个三位数t=![]() ,且P(t)=0,F(t)=135,求这个三位数.
,且P(t)=0,F(t)=135,求这个三位数.
【答案】(1)594;(2)满足条件的三位数为404或440.
【解析】
(1)直接利用原数的差数的定义计算即可得出结论;
(2)先根据原数的积数确定出a=0或b=0,再分两种情况,利用原数的差数为135建立方程求解,即可得出结论.
(1)根据原数的差数的定义得,F(258)=852﹣258=594,
故答案为:594;
(2)根据原数的积数的定义得,P![]() =4ab,
=4ab,
∵P(t)=0,
∴4ab=0,
∴a=0或b=0,
①当a=0时,
Ⅰ、当b≥4时,
∵F(t)=100b+40﹣400﹣b=99b﹣360,
∵F(t)=135,
∴99b﹣360=135,
∴b=![]() =4,满足题意,
=4,满足题意,
即:三位数为:404
Ⅱ、当b<4时,F(t)=400+10b﹣100b﹣4=396﹣90b=135,
∴b=![]() ,此时,b不是整数,不满足题意,
,此时,b不是整数,不满足题意,
②当b=0时,
Ⅰ、当a≥4时,F(t)=100a+40﹣400﹣a=99a﹣360=135,
∴a=4,
即:三位数为:440,
Ⅱ、当a<4时,F(t)=400+10a﹣100a﹣4=396﹣90a=135,
∴b=![]() ,此时,b不是整数,不满足题意,
,此时,b不是整数,不满足题意,
即:满足条件的三位数为404或440.


科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(﹣2,0),B(0,1).
(1)求直线l的函数表达式;
(2)若P是x轴上的一个动点,请直接写出当△PAB是等腰三角形时P的坐标;
(3)在y轴上有点C(0,3),点D在直线l上,若△ACD面积等于4,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,OM和ON分别平分∠AOC和∠BOC.
(1)如图:若C为∠AOB内一点,探究∠MON与∠AOB的数量关系;
(2)若C为∠AOB外一点,且C不在OA、OB的反向延长线上,请你画出图形,并探究∠MON与∠AOB的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
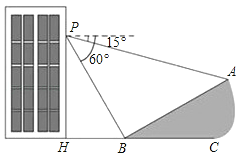
(1)山坡AB的坡度为 ;
(2)若山坡AB的长为20米,求大楼的窗口P处距离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式M=(a+b+1)x3+(2a﹣b)x2+(a+2b)x﹣4是关于x的二次多项式.
(1)若方程3(a+b)y=ky﹣8的解是y=4,求k的值;
(2)当x=2时,代数式M的值为﹣34.当x=﹣2时,求代数式M的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连结AC,将△ACE沿AC翻转得到△ACF,直线FC与直线AB相交于点G.
(1)求证:FG是⊙O的切线;
(2)若B为OG的中点,CE=![]() ,求⊙O的半径长;
,求⊙O的半径长;
(3)①求证:∠CAG=∠BCG;
②若⊙O的面积为4π,GC=2![]() ,求GB的长.
,求GB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
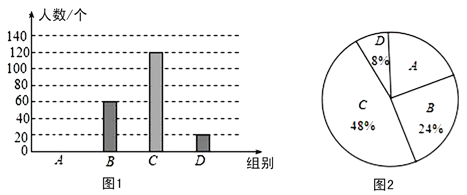
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 匀速运动;点
匀速运动;点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的路径匀速运动.两点同时出发,在
的路径匀速运动.两点同时出发,在![]() 点处首次相遇后,点
点处首次相遇后,点![]() 的运动速度每秒提高了
的运动速度每秒提高了![]() ,并沿
,并沿![]() 的路径匀速运动;点
的路径匀速运动;点![]() 保持速度不变,继续沿原路径匀速运动,某一时刻两点在长方形
保持速度不变,继续沿原路径匀速运动,某一时刻两点在长方形![]() 某一边上的
某一边上的![]() 点处第二次相遇.若点
点处第二次相遇.若点![]() 的速度为
的速度为![]() .
.
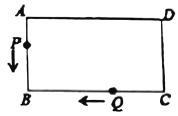
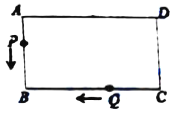
备用图
(1)点![]() 原来的速度为___________
原来的速度为___________![]() .
.
(2)![]() ,
,![]() 两点在
两点在![]() 点处首次相遇后,再经过___________秒后第二次在
点处首次相遇后,再经过___________秒后第二次在![]() 点相遇.
点相遇.
(3)![]() 点在___________边上.此时
点在___________边上.此时![]() ___________
___________![]() .
.
(4)在![]() 点相遇后
点相遇后![]() ,
,![]() 两点沿原来的方向继续前进.又经历了
两点沿原来的方向继续前进.又经历了![]() 次相遇后停止运动,请问此时两点停在长方形
次相遇后停止运动,请问此时两点停在长方形![]() 边上的什么位置?
边上的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
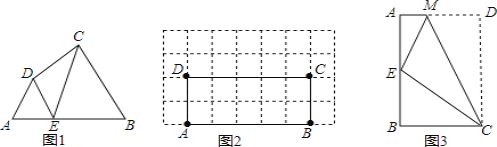
【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com