
【题目】已知代数式M=(a+b+1)x3+(2a﹣b)x2+(a+2b)x﹣4是关于x的二次多项式.
(1)若方程3(a+b)y=ky﹣8的解是y=4,求k的值;
(2)当x=2时,代数式M的值为﹣34.当x=﹣2时,求代数式M的值.
【答案】(1)k=﹣1;(2)-38.
【解析】
(1)根据二次多项式的定义表示出a、b的关系,再把y=4代入方程得到关于k的一元一次方程,然后求解即可;
(2)把x=2代入M得到一个关于a、b的方程,然后联立a+b+1=0解方程组求出a、b的值,然后求出M,再把x=﹣2代入M进行计算即可得解.
(1)∵代数式M=(a+b+1)x3+(2a﹣b)x2+(a+2b)x﹣5是关于x的二次多项式,
∴a+b+1=0,且2a﹣b≠0,
∵关于y的方程3(a+b)y=ky﹣8的解是y=4,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:k=﹣1;
(2)∵当x=2时,代数式M=(2a﹣b)x2+(a+2b)x﹣4的值为﹣34,
∴将x=2代入,得![]() ,
,
整理,得a=﹣3,
∵a+b+1=0,
∴b=2,
∴![]()
![]() .
.
将x=﹣2代入,得![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
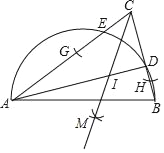
【题目】阅读下面材料:如图,AB是半圆的直径,点D、E在半圆上,且D为弧BE的中点,连接AE、BD并延长,交圆外一点C,按以下步骤作图:
①以点C为圆心,小于BC长为半径画弧,分别交AC、BC于点G、H;
②分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧相交于点M;
GH的长为半径画弧,两弧相交于点M;
③作射线CM,交连接A、D两点的线段于点I.
则点I到△ABC各边的距离_____.(填“相等”或“不等”)
查看答案和解析>>
科目:初中数学 来源: 题型:
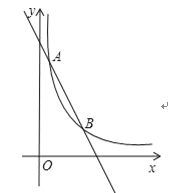
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若任意一个三位数t的百位数字为a,十位数字为b,个位数字为c,那么可将这个三位数表示为t=![]() (a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(1)根据以上材料:F(258)= ;
(2)若一个三位数t=![]() ,且P(t)=0,F(t)=135,求这个三位数.
,且P(t)=0,F(t)=135,求这个三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
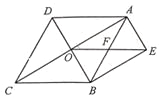
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施. 如图所示,京张高铁起自北京北站,途经清河、沙河、吕平等站,终点站为张家口南站,全长174千米.
(1)根据资料显示,京张高铁的客运价格拟定为0. 4元(人·千米),可估计京张高铁单程票价约为_________元(结果精确到个位);
(2)京张高铁建成后,将是世界上第一条设计时速为350千米/时的高速铁路. 乘高铁从北京到张家口的时间将缩短至1小时,如果按此设计时速运行,那么每站(不计起始站和终点站)停靠的平均时间是多少分钟?(结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com