
【题目】(10分)如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
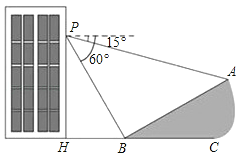
(1)山坡AB的坡度为 ;
(2)若山坡AB的长为20米,求大楼的窗口P处距离地面的高度.
【答案】(1)1:![]() ;(2)大楼的窗口P处距离地面的高度为10
;(2)大楼的窗口P处距离地面的高度为10![]() 米.
米.
【解析】
试题分析:(1)已知山坡的坡角∠ABC=30°,由坡角的正切函数值即为坡度,即可得答案;(2)根据平行线的性质可得∠PBH=∠DPB=60°,再求得∠ABP=180°﹣∠ABC﹣∠PBH=90°.易得△ABP是等腰直角三角形,所以BP=AB=20米,然后在Rt△PBH中利用三角函数即可求解即可.
试题解析:解:(1)∵山坡的坡角∠ABC=30°,
∴山坡AB的坡度为tan30°=![]() =1:
=1:![]() ;
;
(2)由题意得PD∥HC,AB⊥BP,PH⊥HC,∠DPA=15°,∠DPB=60°,AB=20米.
∵PD∥HC,
∴∠PBH=∠DPB=60°,
∴∠ABP=180°﹣∠ABC﹣∠PBH=180°﹣30°﹣60°=90°.
在Rt△ABP中,∵∠ABP=90°,∠APB=60°﹣15°=45°,
∴BP=AB=20米,
在Rt△PBA中,∵∠PHB=90°,∠PBH=60°,
∴PH=PBsin∠PBH=20×![]() =10
=10![]() (米).
(米).
答:大楼的窗口P处距离地面的高度为10![]() 米.
米.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣1,﹣3),C(3,n),交y轴于点B,交x轴于点D.
的图象交于点A(﹣1,﹣3),C(3,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,……按照此规律继续下去,则S2019的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边CD的中点.
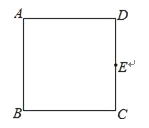
(1)用直尺和圆规作⊙O,使⊙O经过点A、B、E(保留作图痕迹,不写作法);
(2)若正方形ABCD的边长为2,求(1)中所作⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若任意一个三位数t的百位数字为a,十位数字为b,个位数字为c,那么可将这个三位数表示为t=![]() (a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(1)根据以上材料:F(258)= ;
(2)若一个三位数t=![]() ,且P(t)=0,F(t)=135,求这个三位数.
,且P(t)=0,F(t)=135,求这个三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)“校园手机”现象越来越受到社会的关注,小记者刘红随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如下的统计图:
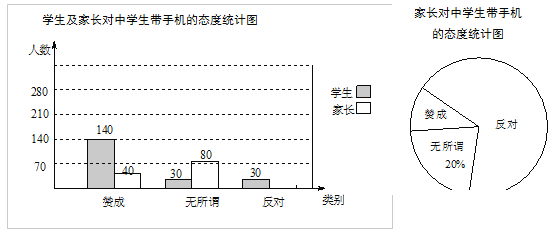
(1)求这次调查的总人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)针对随机调查的情况,刘红决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小丁的家长,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学单元测试,七年级第一小组共10名同学,小组长把超过班级平均分的部分记为“+”,不足的部分记为“-”,记录如表:
与平均分的差值(分) | -15 | -9 | 0 | +3 | +12 | +17 |
人数 | 1 | 2 | 1 | 2 | 3 | 1 |
根据表格数据解答下列问题:
(1)第一小组同学的平均分比班级平均分高还是低?高或低多少分?
(2)若该班这次测试的平均分为80分,求第一小组10名同学的总分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com