【题目】如图，一次函数y＝kx+b的图象与反比例函数y＝
的图象交于点A（﹣1，﹣3），C（3，n），交y轴于点B，交x轴于点D．
（1）求反比例函数y＝和一次函数y＝kx+b的表达式；
（2）连接OA，OC．求△AOC的面积．
【答案】（1）y＝
，y＝x﹣2；（2）4.
【解析】
（1）先把A点坐标代入y＝
中求出m得到反比例函数的解析式是y＝，再确定C的坐标，然后利用待定系数法求一次函数解析式；
（2）先确定D（2，0），然后根据三角形面积公式，利用S△AOC＝S△OCD+S△AOD进行计算．
解：（1）把A（﹣1，﹣3）代入y＝得m＝﹣1×（﹣3）＝3，
则反比例函数的解析式是y＝，
当x＝3代入y＝＝1，则C的坐标是（3，1）；
把A（﹣1，﹣3），C（3，1）代入y＝kx+b得
，解得
，
所以一次函数的解析式是：y＝x﹣2；
（2）x＝0，x﹣2＝0，解得x＝2，则D（2，0），
所以S△AOC＝S△OCD+S△AOD＝
×2×（1+3）＝4．
科目：初中数学 来源： 题型：
【题目】我们把大于1的正整数
的三次幂按一定规则“分裂”成若干个连续奇数的和，如
，
，
，…若
分裂后，其中有一个奇数是2019，则的值是（ ）
A.44B.45C.46D.47
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】聪聪参加我市电视台组织的“阳光杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有
个选项，第二道单选题有4个选项，这两道题聪聪都不会，不过聪聪还有两个“求助”可以用（使用“求助”一次可以让主持人去掉其中一题的一个错误选项）．
（1）如果聪聪两次“求助”都在第一道题中使用，那么聪聪通关的概率是 ．
（2）如果聪聪将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=kx+b经过点A（5，0），B（1，4）．
（1）求直线AB的解析式；
（2）若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式2x﹣4≥kx+b的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正三角形ABC（图1）和正五边形DEFGH（图2）的边长相同．点O为△ABC的中心，用5个相同的△BOC拼入正五边形DEFGH中，得到图3，则图3中的五角星的五个锐角均为（ ）
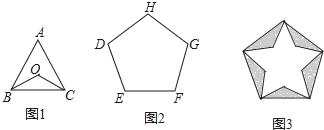
A. 36° B. 42° C. 45° D. 48°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线l：y=kx+b（k≠0）的图象与x轴、y轴交于A、B两点，A（﹣2，0），B（0，1）．
（1）求直线l的函数表达式；
（2）若P是x轴上的一个动点，请直接写出当△PAB是等腰三角形时P的坐标；
（3）在y轴上有点C（0，3），点D在直线l上，若△ACD面积等于4，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为2的正方形ABCD中，点P是边AD上的动点（点P不与点A、点D重合），点Q是边CD上一点，联结PB、PQ，且∠PBC=∠BPQ．
（1）当QD=QC时，求∠ABP的正切值；
（2）设AP=x，CQ=y，求y关于x的函数解析式；
（3）联结BQ，在△PBQ中是否存在度数不变的角？若存在，指出这个角，并求出它的度数；若不存在，请说明理由．
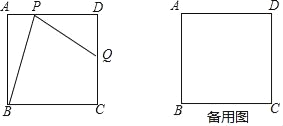
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（10分）如图，小明在大楼的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上，且PH⊥HC．
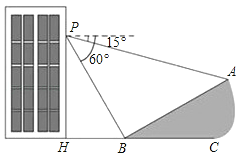
（1）山坡AB的坡度为 ；
（2）若山坡AB的长为20米，求大楼的窗口P处距离地面的高度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
