
【题目】聪聪参加我市电视台组织的“阳光杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有![]() 个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果聪聪两次“求助”都在第一道题中使用,那么聪聪通关的概率是 .
(2)如果聪聪将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
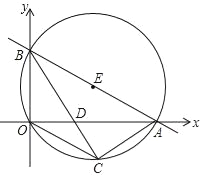
【题目】直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
(1)求A、B、C三点坐标;
(2)求经过O、C、A三点的抛物线解析式;
(3)直线AB上是否存在点P,使得△COP的周长最小?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点E、F、G、H分别是四边形ABCD四条边的中点,若EFGH为菱形,则四边形应具备的下列条件中,不正确的个数是( )
①一组对边平行而另一组对边不平行; ②对角线互相平分;③对角线互相垂直;④对角线相等
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
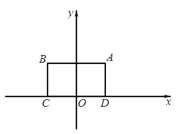
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
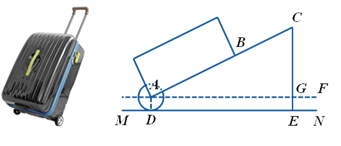
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣1,﹣3),C(3,n),交y轴于点B,交x轴于点D.
的图象交于点A(﹣1,﹣3),C(3,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,A(﹣1,2),B(﹣4,﹣2).
(1)分别作点A,B关于原点的对称点C,D,并写出点C,点D的坐标;
(2)依次连接AB,BC,CD,DA,并证明四边形ABCD是平行四边形.
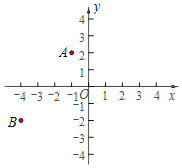
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边CD的中点.
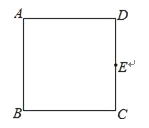
(1)用直尺和圆规作⊙O,使⊙O经过点A、B、E(保留作图痕迹,不写作法);
(2)若正方形ABCD的边长为2,求(1)中所作⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com