
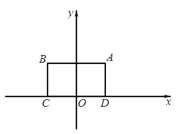
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
【答案】(1) ①![]() ; ②
; ②![]()
![]() 或
或![]()
(2)![]()
【解析】分析:(1)①由点A的坐标为(![]() ,2),顶点C、D在x轴上,且OC=OD,可求得点B,C,D的坐标,继而可求得到此矩形四个顶点距离都相等的点E的坐标,然后由⊙P的半径为4,即可求得答案;
,2),顶点C、D在x轴上,且OC=OD,可求得点B,C,D的坐标,继而可求得到此矩形四个顶点距离都相等的点E的坐标,然后由⊙P的半径为4,即可求得答案;
②首先设P的坐标为(x,-![]() x+1),易得x2+(-
x+1),易得x2+(-![]() x+1-1)2=42,继而求得答案;
x+1-1)2=42,继而求得答案;
(2)由题意可得|m-1|<![]() ,且|m-1|≠0,继而求得答案.
,且|m-1|≠0,继而求得答案.
详解:(1)∵点A的坐标为(![]() ,2),顶点C、D在x轴上,且OC=OD,
,2),顶点C、D在x轴上,且OC=OD,
∴点B的坐标为(-![]() ,2),点C的坐标为(-
,2),点C的坐标为(-![]() ,0),点D的坐标为(
,0),点D的坐标为(![]() ,0),
,0),
∴矩形ABCD的中心E的坐标为(0,1),
当⊙P的半径为4时,
①若P1(0,-3),则PE=1+3=4,
若P2(2![]() ,3),则PE=
,3),则PE=![]() =4,
=4,
若P3(-2![]() ,1)则PE=
,1)则PE=![]() ,
,
∴可以成为矩形ABCD的“等距圆”的圆心的是:P1(0,-3),P2(2![]() ,3);
,3);
故答案为:P1(0,-3),P2(2![]() ,3).
,3).
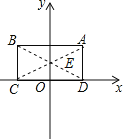
②∵设P的坐标为(x,-![]() x+1),
x+1),
∵E为(0,1),
∴x2+(-![]() x+1-1)2=42,
x+1-1)2=42,
解得:x=±2![]() ,
,
当x=2![]() 时,y=-
时,y=-![]() ×2
×2![]() +1=-1;
+1=-1;
当x=-2![]() 时,y=-
时,y=-![]() ×(-2
×(-2![]() )+1=3;
)+1=3;
∴点P的坐标为(2![]() ,-1)或(-2
,-1)或(-2![]() ,3);
,3);
(2)∵点P在y上,且⊙P是矩形ABCD的“等距圆”,且⊙P与直线AD没有公共点,
∴|m-1|<![]() ,且|m-1|≠0,
,且|m-1|≠0,
解得:1-![]() <m<1+
<m<1+![]() 且m≠1.
且m≠1.
∴点P的纵坐标m的取值范围为:1-![]() <m<1+
<m<1+![]() 且m≠1.
且m≠1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】重庆育才中学需要为老校友们订制![]() 周年纪念吉祥物“陶娃”,原计划订
周年纪念吉祥物“陶娃”,原计划订![]() 份,每份
份,每份![]() 元,订制公司表示:如果多订,可以优惠.根据校庆当天前来的校友数量,学校最终订了
元,订制公司表示:如果多订,可以优惠.根据校庆当天前来的校友数量,学校最终订了![]() 份,并按原价八折购买,但订制公司获得了同样的利润.
份,并按原价八折购买,但订制公司获得了同样的利润.
(1)求订制公司生产每套“陶娃”的成本;
(2)求订制公司获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
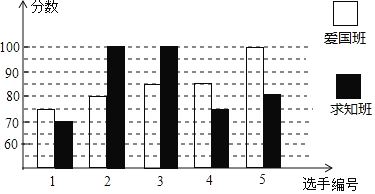
【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把大于1的正整数![]() 的三次幂按一定规则“分裂”成若干个连续奇数的和,如
的三次幂按一定规则“分裂”成若干个连续奇数的和,如![]() ,
,![]() ,
,![]() ,…若
,…若![]() 分裂后,其中有一个奇数是2019,则
分裂后,其中有一个奇数是2019,则![]() 的值是( )
的值是( )
A.44B.45C.46D.47
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聪聪参加我市电视台组织的“阳光杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有![]() 个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果聪聪两次“求助”都在第一道题中使用,那么聪聪通关的概率是 .
(2)如果聪聪将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
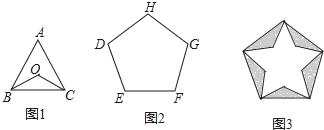
A. 36° B. 42° C. 45° D. 48°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场将一批学生书包按成本价提高50%后标价,又按标价的80%优惠卖出,每个的售价是72元.每个这种书包的成本价是多少元?利润是多少元?利润率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com