
【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

科目:初中数学 来源: 题型:
【题目】今年我市有4万名学生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:
①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000.
其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校七年级男生的体能情况,从该校七年级抽取50名男生进行1分钟跳绳测试,把所得数据整理后,画出频数分布直方图.已知图中从左到右第一、第二、第三、第四小组的频数的比为1:3:4:2.

(1)总体是 ,个体是 ,样本容量是 ;
(2)求第四小组的频数和频率;
(3)求所抽取的50名男生中,1分钟跳绳次数在100次以上(含100次)的人数占所抽取的男生人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
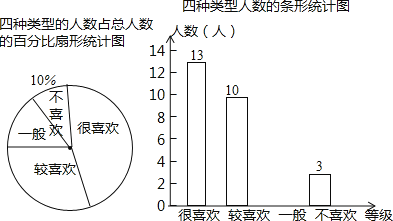
【题目】《中国足球改革总体方案》提出足球要进校园,为了解某校学生对校园足球喜爱的情况,随机对该校部分学生进行了调查,将调查结果分为“很喜欢”、“较喜欢”、“一般”、“不喜欢”四个等级,并根据调查结果绘制成了如下两幅不完整的统计图;
(1)一共调查了 名学生,请补全条形统计图;
(2)在此次调查活动中,选择“一般”的学生中只有两人来自初三年级,现在要从选择“一般”的同学中随机抽取两人来谈谈各自对校园足球的感想,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次数学测验中,随机抽取了10份试卷,其成绩如下:72,77,79,81,81,81,83,83,85,89,则这组数据的众数、中位数分别为( ).
A. 81,82 B. 83,81 C. 81,81 D. 83,82
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间的定价为每天180元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,房价定为多少时,宾馆利润最大?并求出一天的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com