练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某宾馆有50个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，房价定为多少时，宾馆利润最大？并求出一天的最大利润．

    【答案】房价定为350元，宾馆利润最大，一天的最大利润为10890元．

    【解析】

    试题分析：设每个房间每天的定价增加x元，宾馆所得利润为y，从而利用租房利润减去维护费，可得利润函数，利用配方法，即可求得结论．

    解：设每个房间每天的定价增加x元，宾馆所得利润．

    即．

    其中0≤x≤500，且x是10的倍数．

    当时，

    ∴房价定为180+170=350时，宾馆利润最大．

    ∴．

    答：房价定为350元，宾馆利润最大，一天的最大利润为10890元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下面四个结论：（1）AE=BF，（2）AE⊥BF，（3）AO=OE，（4）S△AOB=S四边形DEOF，其中正确结论的序号是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式由左边到右边的变形，是因式分解的是（ ）

    A. 3x(x+y)＝3x2＋3xy B. －2x2－2xy=－2x(x＋y)

    C. (x＋5)(x－5)＝x2－25 D. x2＋x＋1＝x(x＋1)＋1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

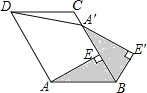
    【题目】如图，已知平行四边形ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x﹣y=2，xy=3，则x2y﹣xy2=______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果a∥b,b∥c,那么a∥c,这个推理的依据是(　　)

    A. 等量代换 B. 平行线的定义

    C. 经过直线外一点,有且只有一条直线与已知直线平行 D. 平行于同一直线的两直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=kx+b的图象与反比例函数y=的图象交于A（﹣2，1），B（1，n）两点．

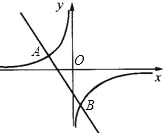
    （1）求反比例函数和一次函数的解析式；

    （2）根据图象写出使一次函数的值＞反比例函数的值的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把长方形纸片ABCD沿EF折叠后．点D与点B重合，点C落在点C′的位置上．若∠1=60°，AE=1．

    （1）求∠2、∠3的度数；

    （2）求长方形纸片ABCD的面积S．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=4cm，AD=12cm，P点在AD边上以每秒1cm的速度从A向D运动，点Q在BC边上，以每秒4cm的速度从C点出发，在CB间往返运动，二点同时出发，待P点到达D点为止，在这段时间内，线段PQ有（ ）次平行于AB．

    A．1 B．2 C．3 D．4

    查看答案和解析>>

    同步练习册答案