
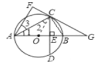
【题目】如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连结AC,将△ACE沿AC翻转得到△ACF,直线FC与直线AB相交于点G.
(1)求证:FG是⊙O的切线;
(2)若B为OG的中点,CE=![]() ,求⊙O的半径长;
,求⊙O的半径长;
(3)①求证:∠CAG=∠BCG;
②若⊙O的面积为4π,GC=2![]() ,求GB的长.
,求GB的长.

【答案】(1)见解析;(2)2;(3) ①见解析; ②2.
【解析】
(1)连接OC,由OA=OC得∠OAC=∠OCA,根据折叠的性质得∠OAC=∠FAC,∠F=∠AEC=90°,则∠OCA=∠FAC,于是可判断OC∥AF,根据平行线的性质得∠OCG=∠F=90°,然后根据切线的性质得直线FC与⊙O相切;
(2)首先证明△OBC是等边三角形,在Rt△OCE中,根据OC2=OE2+CE2,构建方程即可解决问题;
(3)①根据等角的余角相等证明即可;
②利用圆的面积公式求出OB,由△GCB∽△GAC,可得![]() ,由此构建方程即可解决问题;
,由此构建方程即可解决问题;
(1)证明:连结![]() ,则
,则![]() ,
,
![]()
![]()
![]()
又![]() ,
,![]()
即直线![]() 垂直于半径
垂直于半径![]() ,且过
,且过![]() 的外端点
的外端点
![]() 是
是![]() 切线.
切线.
(2)![]() 点
点![]() 是
是![]() 斜边
斜边![]() 的中点,
的中点,![]() ,
,
![]() 是等边三角形,且
是等边三角形,且![]() 是
是![]() 的高。
的高。
在![]() ,
,![]() ,即
,即![]() ,
,
解得![]() ,即
,即![]() 的半径为2.
的半径为2.
(3)①![]() ,
,![]() ,且
,且![]() ,
,
![]() .
.
②![]() ,
,![]() ,由①知:
,由①知:![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,
解得:![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,A(﹣1,2),B(﹣4,﹣2).
(1)分别作点A,B关于原点的对称点C,D,并写出点C,点D的坐标;
(2)依次连接AB,BC,CD,DA,并证明四边形ABCD是平行四边形.
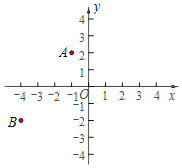
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边CD的中点.
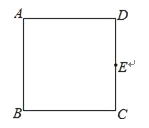
(1)用直尺和圆规作⊙O,使⊙O经过点A、B、E(保留作图痕迹,不写作法);
(2)若正方形ABCD的边长为2,求(1)中所作⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若任意一个三位数t的百位数字为a,十位数字为b,个位数字为c,那么可将这个三位数表示为t=![]() (a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(1)根据以上材料:F(258)= ;
(2)若一个三位数t=![]() ,且P(t)=0,F(t)=135,求这个三位数.
,且P(t)=0,F(t)=135,求这个三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
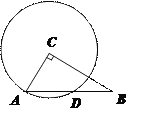
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)“校园手机”现象越来越受到社会的关注,小记者刘红随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如下的统计图:
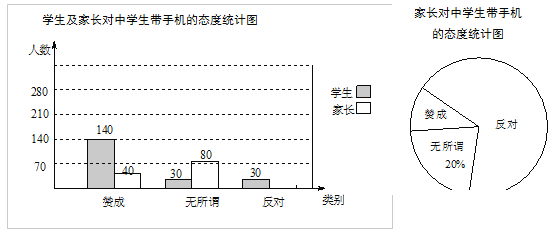
(1)求这次调查的总人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)针对随机调查的情况,刘红决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小丁的家长,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在数轴上标出数﹣4.5,﹣2,1,3.5所对应的点A,B,C,D;
(2)C,D两点间距离=_____;B,C两点间距离=_____;
(3)数轴上有两点M,N,点M对应的数为a,点N对应的数为b,那么M,N两点之间的距离=_____;
(4)若动点P,Q分别从点B,C同时出发,沿数轴负方向运动;已知点P的速度是每秒1个单位长度,点Q的速度是每秒2个单位长度,问①t为何值时P,Q两点重合?②t为何值时P,Q两点之间的距离为1?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①![]() ②若点D是AB的中点,则AF=
②若点D是AB的中点,则AF=![]() AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若
AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若![]() ,则
,则![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )

A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com