
分析 原式第一项变形后利用同底数幂的除法法则计算,第二项利用平方差公式化简,最后一项利用完全平方公式展开,整理得到最简结果,把x与y的值代入计算即可求出值.
解答 解:原式=-(x-2y)2n÷(x-2y)2n-1+(2x-y)(-2x-y)+(x-y)(-x+y)
=-(x-2y)+y2-4x2-x2+2xy-y2
=2xy-5x2-x+2y,
当x=$\frac{1}{3}$,y=$\frac{2}{3}$时,原式=$\frac{4}{9}$-$\frac{5}{9}$-$\frac{1}{3}$+$\frac{4}{3}$=$\frac{8}{9}$.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
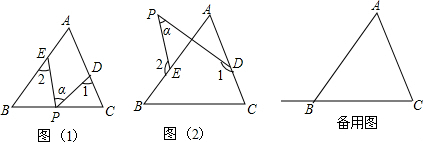
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
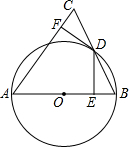 如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com