
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
分析 (1)设甲、乙两种型号的挖掘机各需x台、y台.等量关系:甲、乙两种型号的挖掘机共8台;每小时挖掘土石方540m3;
(2)设租用m辆甲型挖掘机,n辆乙型挖掘机,根据题意列出二元一次方程,求出其正整数解;然后分别计算支付租金,选择符合要求的租用方案.
解答 解:(1)设甲、乙两种型号的挖掘机各需x台、y台.
依题意得:$\left\{\begin{array}{l}{x+y=8}\\{60x+80y=540}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$.
答:甲、乙两种型号的挖掘机各需5台、3台;
(2)设租用m辆甲型挖掘机,n辆乙型挖掘机.
依题意得:60m+80n=540,化简得:3m+4n=27.
∴m=9-$\frac{4}{3}$n,
∴方程的解为$\left\{\begin{array}{l}{m=5}\\{n=3}\end{array}\right.$或$\left\{\begin{array}{l}{m=1}\\{n=6}\end{array}\right.$.
当m=5,n=3时,支付租金:100×5+120×3=860元>850元,超出限额;
当m=1,n=6时,支付租金:100×1+120×6=820元<850元,符合要求.
答:有一种租车方案,即租用1辆甲型挖掘机和6辆乙型挖掘机.
点评 本题考查了一元一次不等式和二元一次方程组的应用.解决问题的关键是读懂题意,依题意列出等式(或不等式)进行求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
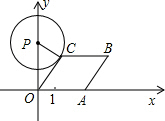 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
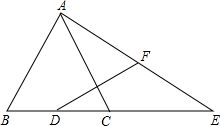 如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.
如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 居民(户) | 1 | 2 | 8 | 6 | 2 | 1 |
| 月用水量(吨) | 4 | 5 | 8 | 12 | 15 | 20 |
| A. | 平均数是10(吨) | B. | 众数是8(吨) | C. | 中位数是10(吨) | D. | 样本容量是20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
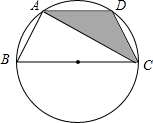 如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$.
如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com