
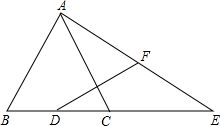
 如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.
如图,已知在△ABC中,AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,D为边BC的中点,E为边BC的延长线上一点,且CE=BC.联结AE,F为线段AE的中点.分析 (1)连接AD,根据等腰三角形性质求出∠ADC=90°,解直角三角形求出AD,求出BD和CD,即可得出答案;
(2)过C作CM⊥AE于M,则∠CMA=∠CME=90°,在Rt△ADE中,由勾股定理求出AE,由勾股定理得出方程(2$\sqrt{5}$)2-AM2=42-(2$\sqrt{13}$-AM)2,求出AM,求出CM,即可求出答案.
解答 解:(1)如图,连接AD,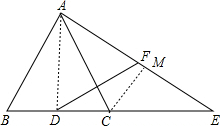
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∵AB=AC=2$\sqrt{5}$,sin∠B=$\frac{2\sqrt{5}}{5}$,
∴$\frac{AD}{AB}$=$\frac{2\sqrt{5}}{5}$,
∴AD=4,
由勾股定理得:BD=2,
∴DC=BD=2,BC=4,
∵CE=BC,
∴CE=4,
∴DE=2+4=6;
(2)过C作CM⊥AE于M,
则∠CMA=∠CME=90°,
在Rt△ADE中,由勾股定理得;AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∵由勾股定理得;CM2=AC2-AM2=CE2-EM2,
∴(2$\sqrt{5}$)2-AM2=42-(2$\sqrt{13}$-AM)2,
解得:AM=$\frac{14\sqrt{13}}{13}$,
CM=$\sqrt{A{C}^{2}-A{M}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-(\frac{14\sqrt{13}}{13})^{2}}$=$\frac{8\sqrt{13}}{13}$,
∴∠CAE的正切值是$\frac{CM}{AM}$=$\frac{\frac{8\sqrt{13}}{13}}{\frac{14\sqrt{13}}{13}}$=$\frac{4}{7}$.
点评 本题考查了等腰三角形的性质,解直角三角形,勾股定理的应用,解此题的关键是构造直角三角形,并进一步求出各个线段的长,有一定的难度.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的半径垂直于弦 | |
| B. | 垂直平分弦的直线必经过圆心 | |
| C. | 垂直于弦的直径平分这条弦所对的弧 | |
| D. | 平分弧的直径垂直平分这条弧所对的弦 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
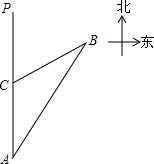 一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com