
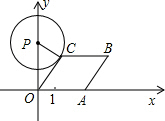
 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$. 分析 分情况讨论①先由切线的性质得出∠OCP=90°,再由已知条件得出∠POC=30°,根据三角函数求出OC,由菱形性质得出OA=OC,即可得出t;②当∠OCP=30°时,圆与OA所在直线相切,同理求得t.
解答 解:∵当以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边OC所在的直线相切,
∴∠OCP=90°,
∵∠AOC=60°,
∴∠POC=30°,
∴OC=OP•cos30°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
∵四边形OABC是菱形,
∴OA=OC=$\frac{3\sqrt{3}}{2}$,
∴t=$\frac{3\sqrt{3}}{2}$-1;
同理当以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边OA所在的直线相切时,求得t=$3\sqrt{3}-1$
故答案为:$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
点评 本题考查了切线的性质、菱形的性质、坐标与图形性质以及锐角三角函数;运用三角函数求出菱形的边长是解决问题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
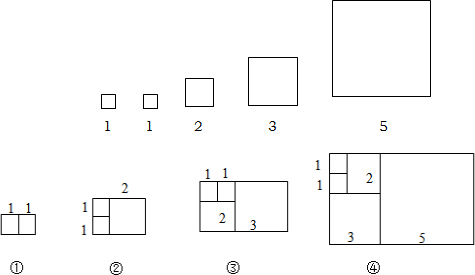
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
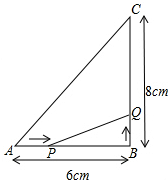 如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的半径垂直于弦 | |
| B. | 垂直平分弦的直线必经过圆心 | |
| C. | 垂直于弦的直径平分这条弦所对的弧 | |
| D. | 平分弧的直径垂直平分这条弧所对的弦 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com