
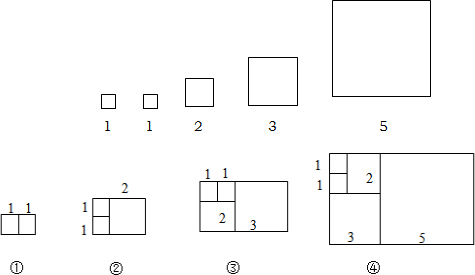
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
分析 结合图形分析表格中图形的周长,①的周长为:2×(1+2),②的周长为:2×(2+3),③的周长为:2×(3+5),④的周长为:2×(5+8),…由此可推出第n个长方形的宽为第n-1个长方形的长,第n个长方形的长为第n-1个长方形的长和宽的和,长方形的周长是前面两个长方形的周长和,由此规律解决问题即可.
解答 解:(1)由分析知:第①个长方形的周长为6=(1+2)×2;
第②个长方形的周长为10=(2+3)×2;
第③个长方形的周长为x=(3+5)×2=16;
第④个长方形的周长为y=(5+8)×2=26;
(2)若按此规律继续拼成长方形,则序号为④的长方形周长是(5+8)×2=26;
(3)①已知序号为n的长方形的周长为a,序号为(n+1)的长方形的周长为b,序号为(n+2)的长方形的周长为a+b,则序号为(n+3)的长方形的周长为b+a+b=a+2b;
②若按此规律继续拼长方形,已知序号为n的长方形的长和宽分别为a、b(其中a<b),序号为n-1的长方形的长和宽分别为b-a、a(其中a<b),则序号为(n+1)的长方形的周长是2(a+b)+2(b-a+a)=2a+4b.
故答案为:16,26;26;a+2b;2a+4b.
点评 此题考查图形的变化规律,要想得到长方形的周长规律,应先找长方形长、宽的变换规律.分析图形中的长和宽,然后结合图表中长方形的周长即可得出长方形周长的变换规律.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
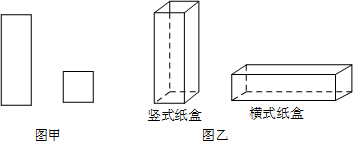
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | 100-x | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
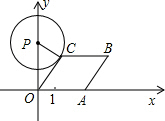 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°.设经过t秒后,以P(0,3)为圆心,PC为半径的圆恰好与菱形OABC的边所在的直线相切,则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com