
分析 作CE⊥AB,根据∠DAB可以求得CE的长,根据CE即可求得AE的长,根据CD=BE=AB-AE即可解题.
解答 解:作CE⊥AB,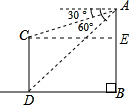
∵∠DAB=90°-60°=30°,
tan30°=$\frac{\sqrt{3}}{3}$,
∴CE=BD=$\frac{\sqrt{3}}{3}$×AB=20$\sqrt{3}$(米),
∵∠ACE=30°,
∴AE=CEtan30°=20$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=20(米),
∴CD=BE=AB-AE=60-20=40(米),
故答案为:40米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形,利用三角函数的知识求解.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
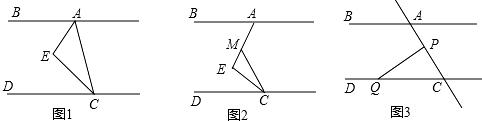
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的半径垂直于弦 | |
| B. | 垂直平分弦的直线必经过圆心 | |
| C. | 垂直于弦的直径平分这条弦所对的弧 | |
| D. | 平分弧的直径垂直平分这条弧所对的弦 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
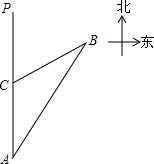 一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 乐山 | 眉山 | 西昌 | 成都 | 德阳 | 绵阳 | 广安 | 南充 | 宜宾 | 广汉 | 遂宁 |
| 28 | 28 | 31 | 28 | 27 | 28 | 27 | 26 | 30 | 28 | 27 |
| A. | 31℃,28℃ | B. | 26℃,28℃ | C. | 5℃,27℃ | D. | 5℃,28℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com