
【题目】关于x的一元二次方程x2﹣ ![]() x+sinα=0有两个相等的实数根,则锐角α等于( )
x+sinα=0有两个相等的实数根,则锐角α等于( )
A.15°
B.30°
C.45°
D.60°
【答案】B
【解析】解:∵关于x的一元二次方程x2﹣ ![]() x+sinα=0有两个相等的实数根, ∴△=
x+sinα=0有两个相等的实数根, ∴△= ![]() ﹣4sinα=2﹣4sinα=0,解得:sinα=
﹣4sinα=2﹣4sinα=0,解得:sinα= ![]() ,
,
∵α为锐角,
∴α=30°.
故选B.
【考点精析】根据题目的已知条件,利用求根公式和特殊角的三角函数值的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一
a | b | c |
3 | 4 | 5 |
5 | 12 | 13 |
7 | 24 | 25 |
9 | 41 |
表二
a | b | c |
6 | 8 | 10 |
8 | 15 | 17 |
10 | 24 | 26 |
12 | 41 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是 ,a、b、c之间的数量关系是 ;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是 ,a、b、c之间的数量关系是 ;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,b=
,b= 时,斜边c的值.
时,斜边c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) 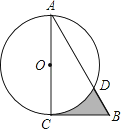
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
![]()
D.![]() ﹣
﹣ ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图,南北方向线MN以西为我国领海,以东为公海.上午9时50分,我缉私艇A发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海驶来,便立即通知正在MN线上巡逻的缉私艇B.已知A,C两艇的距离是13海里,A,B两艇的距离是5海里,缉私艇B与C艇的距离是12海里,若C艇的速度不变,那么它最早会在什么时间进入我国领海?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )
A.方差是20
B.众数是88
C.中位数是86
D.平均数是87
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com