
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
【答案】
(1)
解:令y=0,解得x1=﹣1或x2=3
∴A(﹣1,0)B(3,0)
将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3
∴C(2,﹣3)
∴直线AC的函数解析式是y=﹣x﹣1
(2)
解:设P点的横坐标为x(﹣1≤x≤2)
则P、E的坐标分别为:P(x,﹣x﹣1)
E(x,x2﹣2x﹣3)
∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当 ![]() 时,PE的最大值=
时,PE的最大值= ![]()
(3)
解:存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+ ![]() ,0),F4(4﹣
,0),F4(4﹣ ![]() ,0).
,0).
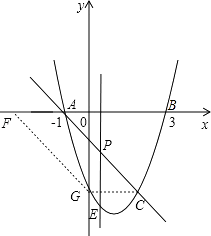
①如图,连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(﹣3,0);
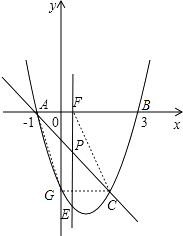
②如图,AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);
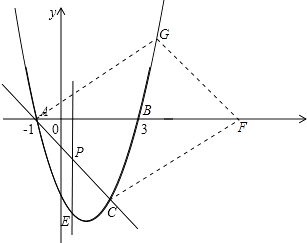
③如图,此时C,G两点的纵坐标互为相反数,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+ ![]() ,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+4+
,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+4+ ![]() .因此直线GF与x轴的交点F的坐标为(4+
.因此直线GF与x轴的交点F的坐标为(4+ ![]() ,0);
,0);
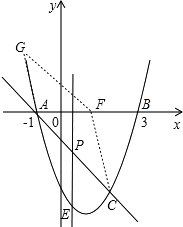
④如图,同③可求出F的坐标为(4﹣ ![]() ,0).
,0).
综合四种情况可得出,存在4个符合条件的F点
【解析】(1)因为抛物线与x轴相交,所以可令y=0,解出A、B的坐标.再根据C点在抛物线上,C点的横坐标为2,代入抛物线中即可得出C点的坐标.再根据两点式方程即可解出AC的函数表达式;(2)根据P点在AC上可设出P点的坐标.E点坐标可根据已知的抛物线求得.因为PE都在垂直于x轴的直线上,所以两点之间的距离为yp﹣yE , 列出方程后结合二次函数的性质即可得出答案;(3)存在四个这样的点.
①连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(﹣3,0);
②AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);
③此时C,G两点的纵坐标关于x轴对称,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+ ![]() ,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+7.因此直线GF与x轴的交点F的坐标为(4+
,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+7.因此直线GF与x轴的交点F的坐标为(4+ ![]() ,0);
,0);
④如图,同③可求出F的坐标为(4﹣ ![]() ,0);
,0);
综合四种情况可得出,存在4个符合条件的F点.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图,在图1所给方格纸中,每个小正方形边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图2中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等.(分割线画成实线.)

(2)如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线L成轴对称的 ![]() ;
;
②请直线L上找到一点P,使得PC + PB的距离之和最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
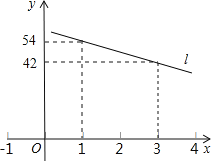
【题目】一辆警车在高速公路的A处加满油,以每小时60千米的速度匀速行驶.已知警车一次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
(1)求直线l的函数关系式;
(2)如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC与△CDA关于点O对称,过O作EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D是关于点O的对应点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称,其中正确的有( )
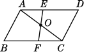
A. 1个 B. 2个 C. 3个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为_____.
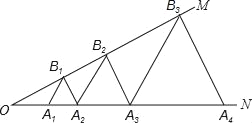
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下: 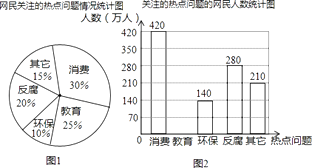
根据以上信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若杭州市约有900万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率为
查看答案和解析>>
科目:初中数学 来源: 题型:
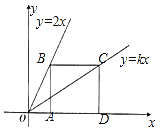
【题目】如图,点B、C分别在直线y=2x和y=kx上,点A、D是x轴上的两点,且四边形ABCD是正方形.
(1)若正方形ABCD的边长为2,则点B、C的坐标分别为 .
(2)若正方形ABCD的边长为a,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com