
【题目】解下列方程:
(1)2x2+3=7x;
(2)(x+4)2=5(x+4);
(3)x2﹣5x+1=0(用配方法);
(4)2x2﹣2 ![]() x﹣5=0.
x﹣5=0.
【答案】
(1)解:2x2﹣7x+3=0,
∴(x﹣3)(2x﹣1)=0,
∴x﹣3=0或2x﹣1=0,
解得:x=3或x= ![]()
(2)解:∵(x+4)2﹣5(x+4)=0,
(x+4)(x﹣1)=0,
∴x+4=0或x﹣1=0,
解得:x=﹣4或x=1
(3)解:x2﹣5x=﹣1,
x2﹣5x+ ![]() =﹣1+
=﹣1+ ![]() ,
,
即(x﹣ ![]() )2=
)2= ![]() ,
,
∴x﹣ ![]() =±
=± ![]() ,
,
即x1= ![]() ,x2=
,x2= ![]()
(4)解:2x2﹣2 ![]() x﹣5=0,
x﹣5=0,
∵a=2,b=﹣2 ![]() ,c=﹣5,
,c=﹣5,
∴△=8+4×2×5=48>0,
∴x= ![]() =
= ![]()
【解析】(1)因式分解法求解可得;(2)提取公因式法求解可得;(3)配方法求解即可得;(4)公式法求解可得.
【考点精析】本题主要考查了配方法和因式分解法的相关知识点,需要掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) 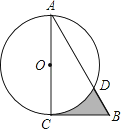
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
![]()
D.![]() ﹣
﹣ ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为一工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.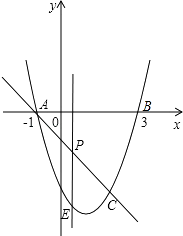
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
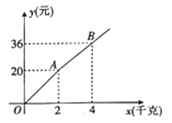
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com