
【题目】解下列方程:
(1)2x2+3=7x;
(2)(x+4)2=5(x+4);
(3)x2﹣5x+1=0(用配方法);
(4)2x2﹣2 ![]() x﹣5=0.
x﹣5=0.
【答案】
(1)解:2x2﹣7x+3=0,
∴(x﹣3)(2x﹣1)=0,
∴x﹣3=0或2x﹣1=0,
解得:x=3或x= ![]()
(2)解:∵(x+4)2﹣5(x+4)=0,
(x+4)(x﹣1)=0,
∴x+4=0或x﹣1=0,
解得:x=﹣4或x=1
(3)解:x2﹣5x=﹣1,
x2﹣5x+ ![]() =﹣1+
=﹣1+ ![]() ,
,
即(x﹣ ![]() )2=
)2= ![]() ,
,
∴x﹣ ![]() =±
=± ![]() ,
,
即x1= ![]() ,x2=
,x2= ![]()
(4)解:2x2﹣2 ![]() x﹣5=0,
x﹣5=0,
∵a=2,b=﹣2 ![]() ,c=﹣5,
,c=﹣5,
∴△=8+4×2×5=48>0,
∴x= ![]() =
= ![]()
【解析】(1)因式分解法求解可得;(2)提取公因式法求解可得;(3)配方法求解即可得;(4)公式法求解可得.
【考点精析】本题主要考查了配方法和因式分解法的相关知识点,需要掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势才能正确解答此题.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】小明家(记为A)、他上学的学校(记为B)、书店(记为C)依次坐落在一条东西走向的大街上,小明家位于学校西边250米处,书店位于学校东边100米处,小明中午放学后,到书店买本辅导书,然后回家吃中午饭,下午直接去学校上课.
(1)试用数轴表示出小明家(A)、学校(B)、书店(C)的位置;
(2)计算出小明家与书店的距离;
(3)小明从中午放学离校到下午上学到校一共走了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅在浏览某电影评价网站时,搜索了最近关注到的甲、乙、丙三部电影,网站通过对观众的抽样调查,得到这三部电影的评分数据统计图分别如下:
甲、乙、丙三部电影评分情况统计图
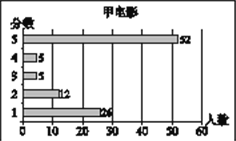


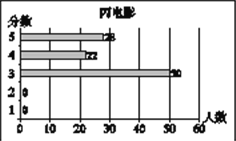
根据以上材料回答下列问题:
(1)小梅根据所学的统计知识,对以上统计图中的数据进行了分析,并通过计算得到这三部电影抽样调查的样本容量,观众评分的平均数、众数、中位数,请你将下表补充完整:
甲、乙、丙三部电影评分情况统计表
电影 | 样本容量 | 平均数 | 众数 | 中位数 |
甲 | 100 | 3.45 | 5 | |
乙 | 3.66 | 5 | ||
丙 | 100 | 3 | 3.5 |
(2)根据统计图和统计表中的数据,可以推断其中_______电影相对比较受欢迎,理由是
_______________________________________________________________________.(至少从两个不同的角度说明你推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 ![]() 与
与 ![]() 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与 ![]() 轴交于点C(0,-3),顶点为D。
轴交于点C(0,-3),顶点为D。
(1)求抛物线的解析式及顶点D的坐标。
(2)联结AC,BC,求∠ACB的正切值。
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由。
(4)M是抛物线上一点,点N在 ![]() 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆警车在高速公路的A处加满油,以每小时60千米的速度匀速行驶.已知警车一次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.
(1)求直线l的函数关系式;
(2)如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是多少?
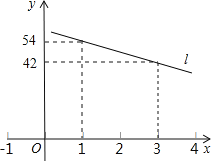
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE. 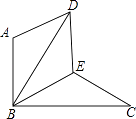
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
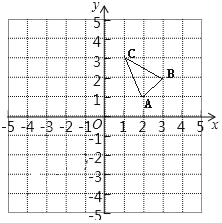
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)将△A1B1C1绕原点O逆时针旋转90°得到△A2B2C2,请画出旋转后的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为圆心的弧 ![]() 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB. 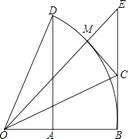
(1)求 ![]() 的值;
的值;
(2)若OE与 ![]() 交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com