
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) 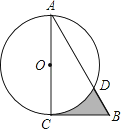
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
![]()
D.![]() ﹣
﹣ ![]()
![]()
【答案】A
【解析】解:如图连接OD、CD.
∵AC是直径,
∴∠ADC=90°,
∵∠A=30°,
∴∠ACD=90°﹣∠A=60°,
∵OC=OD,
∴△OCD是等边三角形,
∵BC是切线.
∴∠ACB=90°,∵BC=2 ![]() ,∴AB=4
,∴AB=4 ![]() ,AC=6,
,AC=6,
∴S阴=S△ABC﹣S△ACD﹣(S扇形OCD﹣S△OCD)
= ![]() ×6×2
×6×2 ![]() ﹣
﹣ ![]() ×3×
×3× ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×32)=
×32)= ![]() ﹣
﹣ ![]() π.
π.
故选A.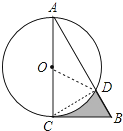
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣ ![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.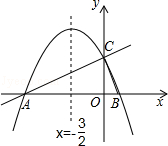
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家(记为A)、他上学的学校(记为B)、书店(记为C)依次坐落在一条东西走向的大街上,小明家位于学校西边250米处,书店位于学校东边100米处,小明中午放学后,到书店买本辅导书,然后回家吃中午饭,下午直接去学校上课.
(1)试用数轴表示出小明家(A)、学校(B)、书店(C)的位置;
(2)计算出小明家与书店的距离;
(3)小明从中午放学离校到下午上学到校一共走了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 . 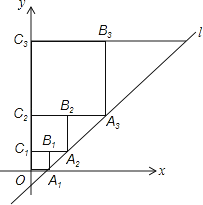
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)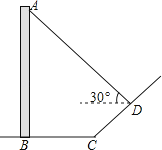
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅在浏览某电影评价网站时,搜索了最近关注到的甲、乙、丙三部电影,网站通过对观众的抽样调查,得到这三部电影的评分数据统计图分别如下:
甲、乙、丙三部电影评分情况统计图
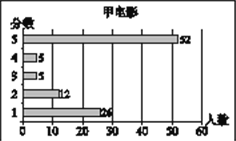


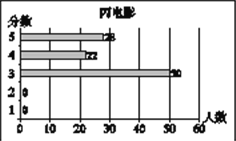
根据以上材料回答下列问题:
(1)小梅根据所学的统计知识,对以上统计图中的数据进行了分析,并通过计算得到这三部电影抽样调查的样本容量,观众评分的平均数、众数、中位数,请你将下表补充完整:
甲、乙、丙三部电影评分情况统计表
电影 | 样本容量 | 平均数 | 众数 | 中位数 |
甲 | 100 | 3.45 | 5 | |
乙 | 3.66 | 5 | ||
丙 | 100 | 3 | 3.5 |
(2)根据统计图和统计表中的数据,可以推断其中_______电影相对比较受欢迎,理由是
_______________________________________________________________________.(至少从两个不同的角度说明你推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com