Question

【题目】（本题8分）如图，在等边△ABC中，点D，E分别在边BC，AB上，BD=AE，AD与CE交于点F.

(1)求证：AD=CE；

(2)求∠DFC的度数.

Answer 1

【答案】(1)证明见解析 (2)60°

证明：（1）在等边△ABC中，AB=BA，∠B=∠CAE

∴在△ACE和△BAD中

∴△ACE≌△BAD（SAS）

∴AD=CE

（2）∵△ACE≌△BAD（已证）

∴∠BAD=∠ACE，

而∠DFC=∠DAC+∠ACE

∴∠DFC=∠DAC+∠BAD=∠BAC=60°

【解析】试题分析：（1）根据△ABC是等边三角形，得到∠BAC=∠B=60°，AB=AC，再根据AE=BD可以利用SAS证得△AEC≌△BDA，从而证得AD=CE．

（2）根据△AEC≌△BDA得到∠ACE=∠BAD，然后求得∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°，从而求得其正弦值．

试题解析：

证明：（1）在等边△ABC中，AB=BA，∠B=∠CAE

∴在△ACE和△BAD中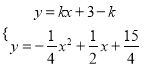

∴△ACE≌△BAD（SAS）

∴AD=CE

（2）∵△ACE≌△BAD（已证）

∴∠BAD=∠ACE，

而∠DFC=∠DAC+∠ACE

∴∠DFC=∠DAC+∠BAD=∠BAC=60°