
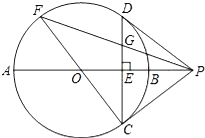
【题目】如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
(1)判断直线PD与⊙O的位置关系,并加以证明;
(2)联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC=![]() ,求EG的长.
,求EG的长.
【答案】(1)PD与⊙![]() 相切于点
相切于点![]() .(2)
.(2)![]()
【解析】试题分析:(1)连接OD,欲证PD是![]() 的切线,只需证明
的切线,只需证明![]() 即可,通过全等三角形
即可,通过全等三角形![]() 的对应角
的对应角![]() 来证明该结论.
来证明该结论.
(2)作![]() 于点M ,先求得
于点M ,先求得![]() ,从而求得
,从而求得![]() ,得出
,得出![]() ,然后证得
,然后证得![]() ,得出
,得出![]() .
.
![]() 中,
中, ![]() ,设
,设![]() ,
, ![]() ,则OC=3
,则OC=3![]() ,进而得出
,进而得出![]() ,从而求的
,从而求的![]() ,
, ![]() ,通过
,通过![]() 得出
得出![]() ,即可求得EG.
,即可求得EG.
试题解析:
(1)证明:联结![]()
∵在⊙![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
,
∴![]() .又∵
.又∵![]() ,∴
,∴![]() ≌
≌![]() .
.
∴![]() .
.
又∵![]() 切⊙
切⊙![]() 于点
于点![]() ,
, ![]() 为⊙
为⊙![]() 半径,
半径,
∴![]() ..
..
∴![]() .∴
.∴![]() .∴
.∴![]() 于点
于点![]() .
.
∴PD与⊙![]() 相切于点
相切于点![]() .
.
(2)作![]() 于点
于点![]() .
.
∵![]() ,
, ![]() 于点
于点![]() ,∴
,∴![]() ,
, ![]() .∴
.∴![]() .
.
∵![]() ,∴Rt△OCE中,
,∴Rt△OCE中, ![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() ,
, ![]() .
.
又∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() ≌
≌![]() .∴
.∴![]() ,
, ![]() .
.
∵在Rt△OCE中, ![]() ,设
,设![]() ,∴
,∴![]() .
.
∴![]() ,
, ![]() .∴
.∴![]() .∴
.∴![]() ,
, ![]() .
.
又∵![]() ,∴
,∴![]() ∥
∥![]() .
.
∴![]() ∽
∽![]() .∴
.∴![]() ,即
,即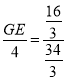 .
.
∴![]() .
.



 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.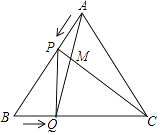
(1)求证:△ABQ≌△CAP;
(2)∠QMC的大小是否发生变化?若无变化,求∠QMC的度数;若有变化,请说明理由;
(3)连接PQ,当点P,Q运动多少秒时,△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,计算正确的是( )
A.(15x2y﹣5xy2)÷5xy=3x﹣5y
B.98×102=(100﹣2)(100+2)=9996
C.![]()
D.(3x+1)(x﹣2)=3x2+x﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路:
如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.
(1)判定△ABD与△AED全等的依据是;
(2)∠ACB与∠ABC的数量关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.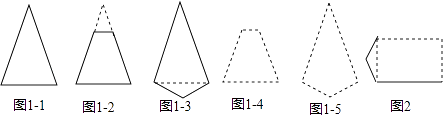
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= ![]() BC,连接CD和EF.
BC,连接CD和EF. 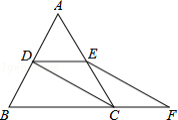
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.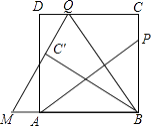
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com