

分析 (1)先根据抛物线的解析式求出抛物线与y轴的交点和对称轴,再根据△ABC的面积求出AB,从而得出点A、B的坐标,最后把点A的坐标代入y=ax2-2ax-4计算即可;
(2)过P作PH⊥x轴于点H,设PH=k,AH=2k,根据tan∠PAB=$\frac{1}{2}$,得出P点的坐标是(2k-2,k)(k>0),再代入抛物线的解析式求出k,即可得出P的坐标;
(3)设AE交y轴于点D,先根据tan∠ACO=tan∠PAB,得出∠PAB=∠ACO,再根据∠ACO+∠OAC=90°,得出PA⊥AC,根据tan∠BCE=$\frac{1}{2}$,得出∠ACE=∠OCB,根据B、C的坐标求出∠OCB=∠ACE=45°和BC的长,根据A、C的坐标得出AC和CE的长,从而证出$\frac{AC}{OC}$=$\frac{CE}{CB}$,再根据∠ACO=∠BCE,证出△ACO∽△EBC,得出∠EBC=∠AOC=90°,从而证出BE⊥BC.
解答 解:(1)∵抛物线y=ax2-2ax-4,
∴与y轴交点C(0,-4),对称轴为直线x=-$\frac{-2a}{2a}$=1,
∴OC=4,
∵抛物线与x轴交于点A、B,且△ABC的面积为12,
∴AB=6,
∴点A(-2,0),B(4,0),
∵抛物线过点A,
∴0=4a+4a-4,
∴a=$\frac{1}{2}$,
∴抛物线表达式为y=$\frac{1}{2}$x2-x-4;
(2)如图1,过P作PH⊥x轴于点H.
设PH=k,AH=2k,
∵tan∠PAB=$\frac{1}{2}$,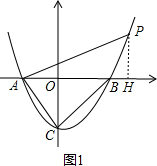
∴P点的坐标是(2k-2,k)(k>0).
∵点P在抛物线上,
∴k=$\frac{1}{2}$(2k-2)2-(2k-2)-4,
∴k=$\frac{7}{2}$,
∴点P的坐标是(5,$\frac{7}{2}$);
(3)如图2,设AE交y轴于点D,
∵A(-2,0),C(0,-4),
∴tan∠ACO=$\frac{1}{2}$,
∵tan∠PAB=$\frac{1}{2}$,
∴∠PAB=∠ACO,
∵∠ACO+∠OAC=90°,
∴∠PAB+∠OAC=90°,
∴PA⊥AC,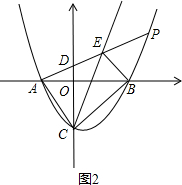
∵tan∠BCE=$\frac{1}{2}$,
∴∠ACO=∠BCE,
∴∠ACE=∠OCB,
∵B(4,0),C(0,-4),
∴∠OCB=∠ACE=45°,BC=4$\sqrt{2}$,
∵A(-2,0),C(0,-4),
∴AO=2,OC=4,
∴AC=2$\sqrt{5}$,
∴CE=2$\sqrt{10}$,
在△AOC和△EBC中,
$\frac{AC}{OC}$=$\frac{2\sqrt{5}}{4}$=$\frac{\sqrt{5}}{2}$,$\frac{CE}{CB}$=$\frac{-2\sqrt{10}}{4\sqrt{2}}$=$\frac{\sqrt{5}}{2}$,
∴$\frac{AC}{OC}$=$\frac{CE}{CB}$,
∵∠ACO=∠BCE,
∴△ACO∽△EBC,
∴∠EBC=∠AOC=90°,
∴BE⊥BC.
点评 此题考查了二次函数的综合,用到的知识点是二次函数的图象与性质、相似三角形的判定与性质、三角形的面积等,关键是根据题意画出图形,作出辅助线,要注意k的取值范围.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-2=$\frac{1}{9}$ | B. | $\sqrt{(-3)^{2}}$=-3 | C. | m6÷m2=m3 | D. | (a-b)2=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 决赛成绩/分 | 95 | 90 | 85 | 80 |
| 人数 | 4 | 6 | 8 | 2 |
| A. | 85,90 | B. | 85,87.5 | C. | 90,85 | D. | 95,90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
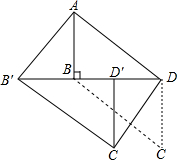 如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.
如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com